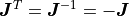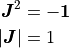シンプレクティック性と解析力学¶
シンプレクティック記法¶
解析力学の特徴は, Hamilton Eq. における一般化座標と共役な運動量 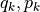 の対称性である.対称性を活かして,N自由度系の状態を2N次元の相空間中の点rで表して,
の対称性である.対称性を活かして,N自由度系の状態を2N次元の相空間中の点rで表して,
![r = \left[ \begin{array}{c}
q_1 \\ q_2 \\ \vdots \\ q_N \\
p_1 \\ p_2 \\ \vdots \\ p_N
\end{array} \right]](../_images/math/942081128edcb34f21e773d93b163171af5d3879.png)
とすれば, Hamilton Eq. は以下の一つの式で表すことができる.
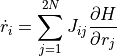
これを シンプレクティック記法 という.
シンプレクティック条件¶
ここで取り扱う シンプレクティック条件 は, シンプレクティック記法における正準変換の条件 である.正準変換の条件は,正準変換の直接条件を満たせばよかった.シンプレクティック条件はより見通しの良い表記になる.
正準変換 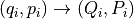 のシンプクレクティック記法
のシンプクレクティック記法 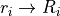 を考える.正準方程式は,
を考える.正準方程式は,
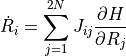
左辺を変形すると,
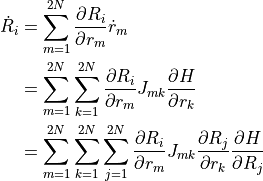
上式と比較し,
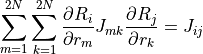
以上より,
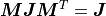
ここで,
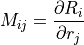
であり, 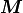 をシンプレクティック行列と呼ぶ.
をシンプレクティック行列と呼ぶ.
以上の, 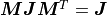 を シンプレクティック条件 という.
を シンプレクティック条件 という.
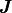
![\bm{J} = \left[ \begin{array}{cc}
\bm{0} & \bm{1} \\
- \bm{1} & \bm{0}
\end{array} \right]](../_images/math/5ed007126d138448e3d5b713a0706a70e1b00e62.png)
![\bm{J}^T = \left[ \begin{array}{cc}
\bm{0} & - \bm{1} \\
\bm{1} & \bm{0}
\end{array} \right] = - \bm{J}](../_images/math/e475a538d93613ae4a7aec93827f819517dcd0a4.png)
![\bm{J} \bm{J}^T = \bm{J}^T \bm{J} = \bm{1} =
\left[ \begin{array}{cc}
\bm{1} & \bm{0} \\
\bm{0} & \bm{1}
\end{array} \right]](../_images/math/78d08de23b4757976167f2fda790098288fda69e.png)