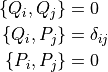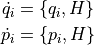ポアッソン括弧による記述¶
ポアッソン括弧 ( Poisson bracket )¶
ハミルトン方程式 ( Hamilton Eq. ) の対称性をさらに向上させるために, ポアッソン括弧 ( Poisson Bracket ) を定義する.
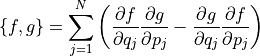
もしくは,行列要素 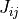 を用いて,
を用いて,
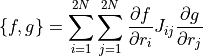
ポアッソン括弧の性質 を以下である.
交換則
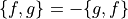
自身との Poisson 括弧はゼロ
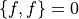
線型性
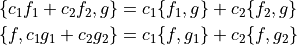
定数との Poisson 括弧はゼロ
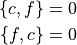
各変数 (位相空間の基底)との Poisson 括弧
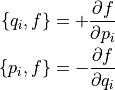
位相空間の基底同士の Poisson 括弧
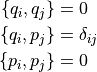
ヤコビ恒等式
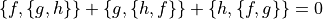
ポアッソン括弧による時間全微分の表現¶
運動系の時間微分は以下のように表される.
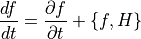
例えば,時間に陽に依存しない ( 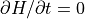 ) ハミルトニアン H の時間全微分は
) ハミルトニアン H の時間全微分は
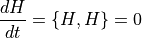
となり, ハミルトニアンは時間的に変化しない ( エネルギー保存則 ).
ポアッソン括弧と運動の関係性¶
ポアッソン括弧は 正準変換に関して不変 である.つまり,
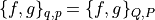
全ての 運動は正準変換 である.ある点から別の点への移動
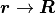 を考える.これは, poisson 括弧による正準変換条件を満たす.つまり, 運動という位相空間変換操作は正準変換 である.
を考える.これは, poisson 括弧による正準変換条件を満たす.つまり, 運動という位相空間変換操作は正準変換 である.物体の運動は, 無限小の連続する正準変換 として表現できる.
生成子がGの無限小の正準変換に対して,ハミルトニアンが対称であれば, Gは保存量 である.
数値積分による,位相空間変換
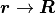 は,一般に正準変換であるとは限らない. ( 一般の数値積分は正準変換でない (力学の運動としての基本条件を満たしていない) )
は,一般に正準変換であるとは限らない. ( 一般の数値積分は正準変換でない (力学の運動としての基本条件を満たしていない) )