ラグランジアンによる運動の記述

ラグランジアン( Lagrangian ) の導入

まず， Lagrangian L の一つの例として以下のようなものが挙げられる．

L = K - U

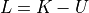
ここで，Kは運動エネルギー，Uはポテンシャルエネルギーであり，Lagrangian は，不定であることに注意されたし．( cf. スカラーポテンシャル・ベクトルポテンシャルの不定性 )

ラグランジュの運動方程式 ( Euler-Lagrange Eqs. )

ラグランジュの運動方程式は，以下の最小作用の原理から，変分法を用いて導出される． ラグランジアン L を一般化座標qに共役な運動量pを用いて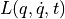， L(q,\dot{q},t) として表して，

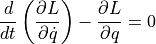
\dfrac{d}{dt} \left( \dfrac{ \partial L }{ \partial \dot{q} }\right) - \dfrac{ \partial L }{ \partial q } = 0

最小作用の原理 ( Hamilton の原理 )

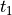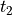時刻 t_1 から t_2 の間の作用積分Sは， Lagrangian 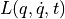L(q,\dot{q},t) を用いて，

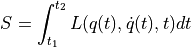
S = \int_{t_1}^{t_2} L(q(t),\dot{q}(t),t) dt

として表す．力学法則は，作用積分Sを最小化する．（こうなるように決まっている．何故かは知らない．これが原理！！）

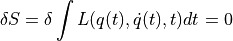
\delta S = \delta \int L(q(t),\dot{q}(t),t) dt = 0

一般化座標に共役な運動量 ( 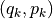(q_k,p_k) ) と循環座標

一般化座標 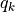q_k に対応する運動量を共役な運動量といい，次の式で表す．

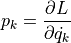
p_k = \dfrac{ \partial L }{ \partial \dot{ q_k } }

ラグランジアン 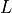L が一般化座標系 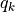q_k に無関係であるとき，一般化座標系 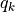q_k を 循環座標 という．つまり，

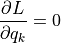
\dfrac{ \partial L }{ \partial q_k } = 0

の時， Euler-Lagrange Eqs. より，

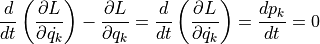
\dfrac{d}{dt} \left( \dfrac{ \partial L }{ \partial \dot{q_k} } \right) - \dfrac{ \partial L }{ \partial q_k } = \dfrac{d}{dt} \left( \dfrac{ \partial L }{ \partial \dot{q_k} } \right) = \dfrac{d p_k }{dt} = 0

より， 循環座標に共役な運動量は保存する ( cf. 軸対称系における角運動量保存則 )．

点変換

座標変換する際に， 全ての座標点が一対一対応し，逆変換が存在する時，これを点変換という ．つまり，

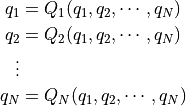
q_1 &= Q_1( q_1, q_2, \cdots, q_N )\\ q_2 &= Q_2( q_1, q_2, \cdots, q_N )\\ \vdots & \\ q_N &= Q_N( q_1, q_2, \cdots, q_N )

で表される一対一の写像．例えば 正則行列による線形写像 では， 一対一対応し，逆変換が存在し，点変換に相当する． つまり，点変換は，逆行列が存在するフルランク写像(正則行列)みたいな（線形変換とは限らないので）変換である．

ラグランジュ方程式の不変性

ラグランジュ方程式 ( Lagrange Eqs. )，

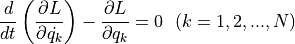
\dfrac{d}{dt} \left( \dfrac{ \partial L }{ \partial \dot{q_k} }\right) - \dfrac{ \partial L }{ \partial q_k } = 0 \ \ ( k=1,2,...,N )

は， 点変換に関して形を変えない ． つまり，任意の一対一の座標変換(点変換)をいくら実行しても， ラグランジュ方程式は常にこの式のままである． 機械的に方程式を立てて，解く際には非常に好ましい性質 である．