解析力学の目的・立ち位置・意義¶

解析力学の目的(私の理解)は，以下の4つ．

系のニュートンの運動方程式を幾何的な考察なしに，機械的に導出する( Better 古典力学としての解析力学 )．
ニュートンの運動方程式を支配するより根源的な原理の探求 ( Hamilton の原理 = 最小作用の原理 )
複雑系であることが不可避な他力学分野( 量子力学，プラズマ物理等 )の記述．
数値的取り扱いにおけるアドバンテージ( シンプレクティック積分 )

解析力学を考える上で重要な見地¶

力学は変数変換が重要¶

力学に限らず， 解析的に解ける問題はごく僅か．
数値的に解く( Newton の運動方程式 = 微分方程式 )を数値積分が役立つ．
解析的に解くにしても，数値的に解くしても， 変数変換は以下のような利点がある ため，解析において極めて重要．
1. 変数の数を減らす ことができる
2. 方程式の 特異性を除去 したり，解析的に解けるように( 可積分系へ変更 )したり
3. 物理的意味をわかりやすく したりできる．
適用する座標系，変数によって，運動方程式が変更される( cf. 見かけの力：遠心力，コリオリ力 )が生じると面倒．できれば座標系や変数の選び方によらずに支配方程式が一定であれば，楽に運動の記述，及び，解析ができる．

解析力学の戦略１．Euler-Lagrange 方程式による解法¶

系の運動エネルギーとポテンシャルから，ラグランジアン 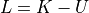$L=K-U$ を計算する．
Euler-Lagrange Eqs. を使用して，解くべき方程式を導出．
解くべき方程式を 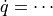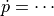$\dot{q}=\cdots$ , $\dot{p}=\cdots$ の形へ変形する．
4th-order Runge-Kutta etc. により，数値積分する．

解析力学の戦略２． Hamilton 方程式による解法 (古典)¶

系の運動エネルギーKとポテンシャルU， Lagrangian L からハミルトニアン 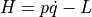$H=p\dot{q}-L$ を計算する．
正準方程式 ( Hamilton Eqs. ) から方程式を導出する．
4th-order Runge-Kutta etc. により，数値積分する．

解析力学の戦略３． Hamilton 方程式による解法 (解析力学)¶

系の運動エネルギーKとポテンシャルU， Lagrangian L からハミルトニアン 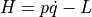$H=p\dot{q}-L$ を計算する．
正準方程式 ( Hamilton Eqs. ) から方程式を導出する．
シンプレクティック数値積分法により，数値積分する．