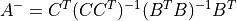一般逆行列について¶
線型連立方程式における解の種類:逆行列の存在¶
線型連立方程式
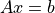
に対して,解 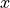 を求める手法には,Cramerの公式や余因子や掃出法等,複数存在する.逆行列を求めることにより,
を求める手法には,Cramerの公式や余因子や掃出法等,複数存在する.逆行列を求めることにより,
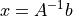
から解を得ることができる. 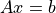 と表記される全ての場合で,解が存在する訳ではない.
行列
と表記される全ての場合で,解が存在する訳ではない.
行列 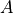 の形状 (
の形状 ( 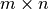 ),及び,階数(
),及び,階数( 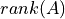 ) によってこれらの振る舞いは変化し,逆行列の存在が左右される.
) によってこれらの振る舞いは変化し,逆行列の存在が左右される.
行列の形状,階数によって,以下の4つに分類される.
行列
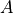 は
は 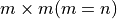 正方行列で,
正方行列で, 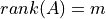 (フルランク)である.
(フルランク)である.行列
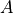 は
は 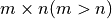 縦長行列で,
縦長行列で, 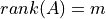 (フルランク)である.
(フルランク)である.行列
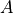 は
は 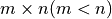 横長行列で,
横長行列で, 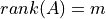 (フルランク)である.
(フルランク)である.フルランクでない.( 行列
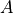 の階数が
の階数が 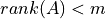 )
)
これらの解は次のように表現される.
逆行列
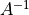 を求めることができ,一意に解が決定される.(決定系)
を求めることができ,一意に解が決定される.(決定系)全ての解を無矛盾に満たす解が存在しない.(優決定系・不能)
方程式が不足しているため,解が一意に定まらない(劣決定系・不定)
方程式に重複(矛盾)が存在する.重複を除けば(a),(b),(c)のどれかに帰着する.
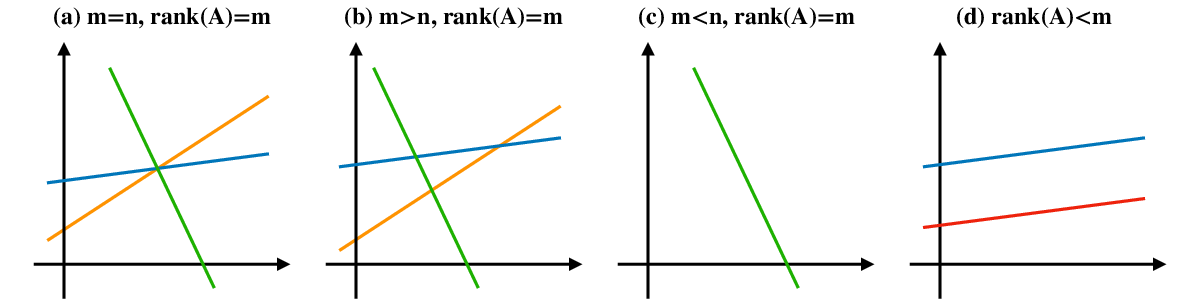
ここでは(a)以外は解を一意に決定できない.これら方程式の解を得る( 存在しないものもあるが,極力合理的に解らしきものを採用する )戦略は次である.
逆行列
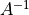 を求めて,
を求めて, 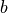 にかけ,
にかけ, 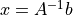 を求める. ( 決定解 )
を求める. ( 決定解 )全方程式から平均的に近い解(最小二乗解)を求める. ( 最小二乗解 )
全解候補のうち,もっともノルムの小さいものを求める.( 最小ノルム解 )
全方程式からの「二乗誤差最小」でかつ「ノルムがもっとも小さいもの」を選ぶ.((b)と(c)を両方満たす解)
これをイメージとして表すと,
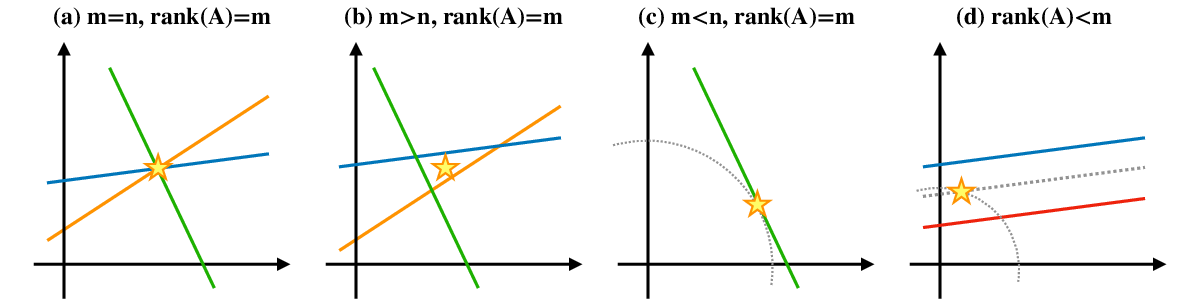
解はそれぞれ,
逆行列から決定解を得る.
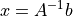
(b) 最小二乗解を得る. 条件式は,
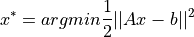
この式は 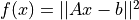 とした際の
とした際の 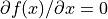 であるから,
であるから,
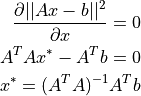
行列( 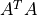 )は正則なnxn対称行列で,
)は正則なnxn対称行列で, 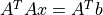 は正規方程式と呼ばれる.
は正規方程式と呼ばれる.
(c) 最小ノルム解 条件式は,
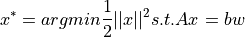
Lagrangeの未定乗数を用いてとけば,
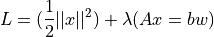
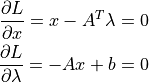
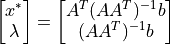
A = BC