線形代数の予備知識:固有値・固有ベクトルと逆問題¶
固有値・固有ベクトル¶
行列 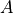 を考えた時,行列
を考えた時,行列 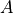 が作る写像には,入力されたベクトル
が作る写像には,入力されたベクトル  を定数倍するような方向が存在し得る.
このある行列に対する特別な方向ベクトルのことを「固有ベクトル」,定数倍を「固有値」という.つまり,
を定数倍するような方向が存在し得る.
このある行列に対する特別な方向ベクトルのことを「固有ベクトル」,定数倍を「固有値」という.つまり,
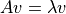
を満たすベクトル  を求めればよく,これを満たすn本の固有ベクトル
を求めればよく,これを満たすn本の固有ベクトル 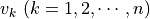 は対応する固有値
は対応する固有値 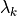 に対して,
に対して,
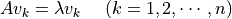
を満たす. 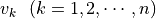 は互いに 線型独立 である.
は互いに 線型独立 である. 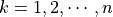 全ての
全ての 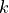 でこの条件を満たすのでn本の固有ベクトルを集めた行列
でこの条件を満たすのでn本の固有ベクトルを集めた行列 ![V=[v_1,v_2,\cdots,v_n]](../_images/math/031753a902927db98e7c76344f0b5e22879087a7.png) を用いて,
を用いて,
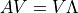
と表現することができる.ここで対角行列 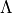 は,
は,
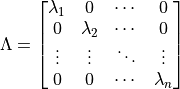
である.
行列 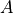 の対角化,対角行列
の対角化,対角行列 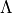 は,
は,
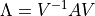
逆に,行列 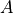 は対角行列
は対角行列 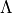 を用いて,
を用いて,
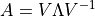
と表現することができる.行列 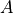 の対角化表示
の対角化表示 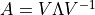 を求めることができた.
を求めることができた.
固有値・固有ベクトルと逆行列¶
固有値・固有ベクトルが既知であれば,これらを利用して 行列反転 (つまりは 逆行列 )を計算することができる.まず,行列反転する対象となる連立方程式を
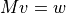
と書いておく.
ここで, 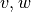 は
は 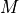 の線型独立な固有ベクトル
の線型独立な固有ベクトル 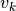 を用いた線型結合で表すことができて,
を用いた線型結合で表すことができて,
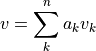
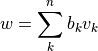
と書ける. 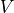 を用いて,行列-ベクトル積の形式で書けば,
を用いて,行列-ベクトル積の形式で書けば,
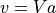
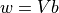
である. 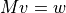 へ代入することで,
へ代入することで,
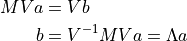
k成分を考えれば,
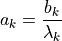
が得られる.もし, 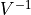 が既知であれば,
が既知であれば,
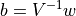
から, 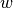 の線型結合の係数
の線型結合の係数 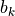 をまとめた
をまとめた 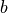 を求めることができ,これを用いて,
を求めることができ,これを用いて,
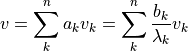
から行列反転( 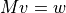 から
から  を求める操作 )を行うことができる.線型結合を用いて,くどく書かれているが,これはつまり,
を求める操作 )を行うことができる.線型結合を用いて,くどく書かれているが,これはつまり,
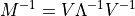
を計算しているのと等価である.
Note
固有値,固有ベクトルが分かっていれば,逆行列を直接求めなくとも, 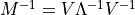 により,逆行列を求めることができる .行列反転に帰着されていた逆問題にとって, 固有値・固有ベクトルが計算上の強力なツールとなり得る.
により,逆行列を求めることができる .行列反転に帰着されていた逆問題にとって, 固有値・固有ベクトルが計算上の強力なツールとなり得る.
Note
単に逆行列を演算するのに比較し,対角表示した行列から逆問題を解くことには以下の利点が存在する.
固有値・固有ベクトル毎の成分表示が行える.これは固有値
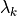 に対応する成分がどの程度強いのかを表示する操作(主成分分析) に相当し,逆問題解析上の利点が生じる.
に対応する成分がどの程度強いのかを表示する操作(主成分分析) に相当し,逆問題解析上の利点が生じる.非正方な行列の演算
