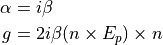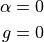ベクトル型 Helmholtz 方程式解析 ( Vectorial Helmholtz Equation )¶
非線形な Poisson 方程式-like な偏微分方程式として、 Helmholtz 方程式がある.Poisson 方程式が
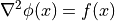
と表されるのに対して、 Helmholtz 方程式は、
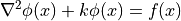
として表される.これは、 Poisson 方程式の左辺項が 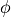 を含むと捉えれば、
を含むと捉えれば、
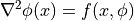
と表現できるので、非線形な Poisson 方程式-likeであると考えることができる. つまり、ある 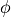 において、方程式を線形化してFEMを用いた解析が可能である
において、方程式を線形化してFEMを用いた解析が可能である
Elmerにおける ベクトル型 Helmholtz 方程式解析¶
周波数領域で電磁場伝搬を考える際に、ベクトル型 Helmholtz を用いて、とある周波数における振幅分布を解析することができる.
FEM解析ソフトウェア Elmer における ベクトル型 Helmholtz 方程式解析は Solver
Procedure = "VectorHelmholtz" "VectorHelmholtzSolver"
を用いて解くことができる.
電磁場の周波数解析における基礎方程式系¶
解析対象となる基礎方程式系は以下となる. Maxwell 方程式より、
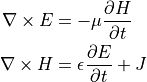
第1式 Faraday's law の curl をとって、第2式を代入すれば、
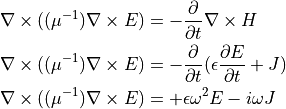
上式により、周波数領域における Maxwell 方程式の Fourier 変換が、Helmholtz 方程式のVector形式である 以下の Vector Helmholtz Equation に帰着することが示される.
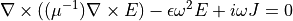
Vectorial Helmholtz Equationの境界条件¶
境界条件を表す式¶
Vectorial Helmholtz Equationの境界条件 ( 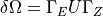 )は、以下の式で与えられる.
)は、以下の式で与えられる.
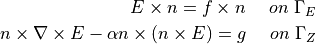
ここで、 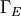 は、導電性の壁条件 ( f=0 で完全導体壁条件 )、
は、導電性の壁条件 ( f=0 で完全導体壁条件 )、 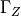 はインピーダンス壁条件である.
はインピーダンス壁条件である.
一般的な境界条件の指針を以下に記す¶
ここで、よく用いられる一般的な境界条件を以下に記す.
リオントヴィッチ・インピーダンス境界条件( Leontovich impedance boundary )
吸収境界条件
単色波を入射させる条件
Neumann 境界条件 ( 自然境界条件 )
完全導体壁条件 ( PEC )
上記、境界条件の設定方法を以下に記す.
リオントヴィッチ・インピーダンス境界条件( Leontovich impedance boundary )¶
境界部分において、とあるインピーダンス ( 電場と電流の1対1関係が成立する) 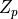 が存在しているとして課される境界条件式. 固定端境界条件 ( = 完全導体壁(PEC) )のうち、マイルドな条件式. 数式で表すと、
が存在しているとして課される境界条件式. 固定端境界条件 ( = 完全導体壁(PEC) )のうち、マイルドな条件式. 数式で表すと、
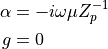
ここで、
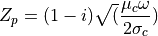
なので、実際上は、
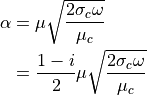
及び、
を指定する.境界条件の指定例は以下である.
Electric Robin Coefficient = Real $ ( 0.5 ) * alp_m
Electric Robin Coefficient im = Real $ ( -0.5 ) * alp_m
Magnetic Boundary Load 2 = Real $ 0.0
Magnetic Boundary Load 2 im = Real $ 0.0
完全導体壁条件 ( PEC )¶
完全導体壁条件 ( PEC )による固定端条件.電磁場は完全反射される.
条件式は、
電場の境界の法線ベクトルに垂直な成分を直接 0 として指定する.
E re {e} = 0.0
E im {e} = 0.0
ベクトル型 Helmholtz 方程式解析の 使用法¶
Equation¶
Angular Frequency
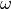 : 必須. 基礎方程式中の角周波数
: 必須. 基礎方程式中の角周波数 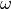 .
.( The angular frequency
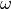 . )
. )
Solver¶
Use Piola Transform Logical
Piola 変換を用いるか、どうか.False で良い.はず.
( Utilize modern Piola transformed edge elements. Increases number of DOFs on meshes containing hexahedral and pyramidal elements. If the mesh contains elements that are not affine images of the reference element, then this option should be enabled. )
( Piola 変換辺要素を使用する.六面体・ピラミッド型のメッシュの自由度をあげる.基準座標系のアフィン写像ではないような要素を含む際( コメント:特殊な形の要素ということ?? )、このオプションを有効にせよ. )
Body Force¶
Current Density i Real :
Current Density im i Real :
もし、必要とあれば.電流密度:基礎方程式中の電流ソース項.
Boundary Condition¶
Electric Robin Coefficient (Real)
Electric Robin Coefficient im (Real)
ロビン境界条件における係数 (
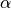 ) :電磁場解析(導波管解析)の境界条件の式を参照のこと
) :電磁場解析(導波管解析)の境界条件の式を参照のことMagnetic Boundary Load (Real)
Magnetic Boundary Load im (Real)
境界条件を指定する関数
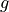 の値. :電磁場解析(導波管解析)の境界条件の式を参照のこと
の値. :電磁場解析(導波管解析)の境界条件の式を参照のこと
具体例¶
具体例については、次項、導波管の解析を参考のこと.
ベクトル型 Helmholtz 方程式解析の注意点¶
現状、私の環境で Mac での使用ができていない.おそらくインストールの不備.Fortranのルーチン実行中にセグフォ、計算条件エラーが排出され、計算できない.Linux 環境では同じ .sif ファイルを使用して計算できたので、インストールに失敗している箇所があるのだと思う.( 特にライブラリ関係とのリンク? )
サンプルが少ない. Elmer Forumにもほとんど存在しない.同梱されている実行テスト用サンプルは同様のものが複数あるが、ほとんど変更がないため、参考にしにくい.Gui Tutorialにも一件あり.しかし、情報は少ない.
上記、 Mac での不具合と境界条件 ( Leontovich's )が直感的に理解しにくかったこと、 完全導体壁条件の指定方法が複数あること、等と相まって、実行にはかなり苦労した.( 実働 3日間ほどかかってしまった.)
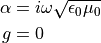
 として、以下を用いる.
として、以下を用いる.