C型電磁石がつくる磁場¶
C型電磁石が作る磁場の解析結果を以下に示す.
問題設定 / メッシュ¶
C型の鉄芯を考える.鉄芯の断面は長さ 0.2 (m) の正方形とし、鉄芯の中心経路は一辺 0.5 (m) とする(つまり、C型電磁石の一辺の合計長さは 0.1+0.5+0.1 = 0.7 (m) となる).
中心経路をつくる正方形のうち、ギャップと反対側の辺にコイルを設置する.コイルはコーナー部を除いた鉄芯直線部分のうち、60 (%) の領域に巻きつける.直線部分は長さ 0.5-0.1-0.1 = 0.3 であるからコイルの巻きつけ長さは 0.3*0.6 = 0.18 であり、コイル幅は 0.02 (m) と設定する.コイル電流は 100 kA とする.
計算領域は、1辺 2.0 (m) の立方体の計算空間を考え、境界で電磁ポテンシャルは Dirichlet 条件
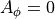 を課す.
を課す.

C型電磁石のメッシュ生成 プログラム¶
メッシュ生成用プログラムを以下に示す.
1import numpy as np
2import os, sys
3import gmsh_api.gmsh as gmsh
4
5import nkGmshRoutines.generate__quadShape as qua
6import nkGmshRoutines.generate__squareTube as tub
7
8
9# ------------------------------------------------- #
10# --- [1] initialization of the gmsh --- #
11# ------------------------------------------------- #
12gmsh.initialize()
13gmsh.option.setNumber( "General.Terminal", 1 )
14gmsh.model.add( "model" )
15
16# ------------------------------------------------- #
17# --- [2] initialize settings --- #
18# ------------------------------------------------- #
19ptsDim , lineDim , surfDim , voluDim = 0, 1, 2, 3
20pts , line , surf , volu = {}, {}, {}, {}
21ptsPhys, linePhys, surfPhys, voluPhys = {}, {}, {}, {}
22x_, y_, z_, lc_, tag_ = 0, 1, 2, 3, 4
23
24# ------------------------------------------------- #
25# --- [3] Modeling --- #
26# ------------------------------------------------- #
27
28lc_sim = 0.800
29lc_mag = 0.010
30lc_coil = 0.010
31
32gap = 0.100
33Lmag = 0.500
34Lsquare = 0.200
35coil_width = 0.020
36
37# ------------------------------------------------- #
38# --- C-shaped Magnet core --- #
39# ------------------------------------------------- #
40
41Ledge_out = 0.5*Lmag + 0.5*Lsquare
42Ledge_inn = 0.5*Lmag - 0.5*Lsquare
43Lhalf_gap = 0.5*gap
44y_minus = - 0.5*Lsquare
45
46pts["x1" ] = [ -Ledge_out, y_minus, -Ledge_out, lc_mag, 0 ]
47pts["x2" ] = [ +Ledge_out, y_minus, -Ledge_out, lc_mag, 0 ]
48pts["x3" ] = [ +Ledge_out, y_minus, -Lhalf_gap, lc_mag, 0 ]
49pts["x4" ] = [ +Ledge_inn, y_minus, -Lhalf_gap, lc_mag, 0 ]
50pts["x5" ] = [ +Ledge_inn, y_minus, -Ledge_inn, lc_mag, 0 ]
51pts["x6" ] = [ -Ledge_inn, y_minus, -Ledge_inn, lc_mag, 0 ]
52pts["x7" ] = [ -Ledge_inn, y_minus, +Ledge_inn, lc_mag, 0 ]
53pts["x8" ] = [ +Ledge_inn, y_minus, +Ledge_inn, lc_mag, 0 ]
54pts["x9" ] = [ +Ledge_inn, y_minus, +Lhalf_gap, lc_mag, 0 ]
55pts["x10"] = [ +Ledge_out, y_minus, +Lhalf_gap, lc_mag, 0 ]
56pts["x11"] = [ +Ledge_out, y_minus, +Ledge_out, lc_mag, 0 ]
57pts["x12"] = [ -Ledge_out, y_minus, +Ledge_out, lc_mag, 0 ]
58
59# -- add points -- #
60for key in list( pts.keys() ):
61 pts[key][4] = gmsh.model.occ.addPoint( pts[key][0], pts[key][1], pts[key][2], meshSize=pts[key][3] )
62
63# -- add lines -- #
64lineLoop = []
65index = [ ik+1 for ik in range(12) ] + [1]
66for ik in range( len( index )-1 ):
67 ik1, ik2 = index[ik], index[ik+1]
68 ptkey1, ptkey2 = "x{0}".format(ik1), "x{0}".format(ik2)
69 linekey = "line_{0}_{1}".format(ik1,ik2)
70 line[linekey] = gmsh.model.occ.addLine( pts[ptkey1][tag_], pts[ptkey2][tag_] )
71 lineLoop.append( line[linekey] )
72
73# -- add surface -- #
74lineGroup = gmsh.model.occ.addCurveLoop( lineLoop )
75surf["cMag"] = gmsh.model.occ.addPlaneSurface( [ lineGroup ] )
76
77# -- add volume -- #
78delta = [ 0.0, Lsquare, 0.0 ]
79ret1 = gmsh.model.occ.extrude( [ (surfDim,surf["cMag"]) ], delta[0], delta[1], delta[2] )
80volu["cMag"] = ret1[1][1]
81
82
83# ------------------------------------------------- #
84# --- coil around magnetic core --- #
85# ------------------------------------------------- #
86
87coil_length = ( Lmag - Lsquare ) * 0.6
88xcent = - 0.5*Lmag
89ycent = 0.0
90d_in = 0.5*Lsquare
91d_out = 0.5*Lsquare + coil_width
92z_bot = - 0.5*coil_length
93z_top = + 0.5*coil_length
94
95vL1_coil_1 = [ xcent-d_out, ycent-d_out, z_bot ]
96vL1_coil_2 = [ xcent-d_in , ycent-d_out, z_bot ]
97vL1_coil_3 = [ xcent-d_in , ycent-d_out, z_top ]
98vL1_coil_4 = [ xcent-d_out, ycent-d_out, z_top ]
99delta1 = [ 0.0, 2.0*d_out, 0.0 ]
100
101vL2_coil_1 = [ xcent-d_in , ycent-d_out, z_bot ]
102vL2_coil_2 = [ xcent+d_in , ycent-d_out, z_bot ]
103vL2_coil_3 = [ xcent+d_in , ycent-d_out, z_top ]
104vL2_coil_4 = [ xcent-d_in , ycent-d_out, z_top ]
105delta2 = [ 0.0, coil_width, 0.0 ]
106
107vL3_coil_1 = [ xcent-d_in , ycent+d_in , z_bot ]
108vL3_coil_2 = [ xcent+d_in , ycent+d_in , z_bot ]
109vL3_coil_3 = [ xcent+d_in , ycent+d_in , z_top ]
110vL3_coil_4 = [ xcent-d_in , ycent+d_in , z_top ]
111delta3 = [ 0.0, coil_width, 0.0 ]
112
113vL4_coil_1 = [ xcent+d_in , ycent-d_out, z_bot ]
114vL4_coil_2 = [ xcent+d_out, ycent-d_out, z_bot ]
115vL4_coil_3 = [ xcent+d_out, ycent-d_out, z_top ]
116vL4_coil_4 = [ xcent+d_in , ycent-d_out, z_top ]
117delta4 = [ 0.0, 2.0*d_out, 0.0 ]
118
119ret2_1 = qua.generate__quadShape( lc=lc_coil, extrude_delta=delta1, defineVolu=True, \
120 x1=vL1_coil_1, x2=vL1_coil_2, \
121 x3=vL1_coil_3, x4=vL1_coil_4 )
122ret2_2 = qua.generate__quadShape( lc=lc_coil, extrude_delta=delta2, defineVolu=True, \
123 x1=vL2_coil_1, x2=vL2_coil_2, \
124 x3=vL2_coil_3, x4=vL2_coil_4 )
125ret2_3 = qua.generate__quadShape( lc=lc_coil, extrude_delta=delta3, defineVolu=True, \
126 x1=vL3_coil_1, x2=vL3_coil_2, \
127 x3=vL3_coil_3, x4=vL3_coil_4 )
128ret2_4 = qua.generate__quadShape( lc=lc_coil, extrude_delta=delta4, defineVolu=True, \
129 x1=vL4_coil_1, x2=vL4_coil_2, \
130 x3=vL4_coil_3, x4=vL4_coil_4 )
131volu["coil1"] = ret2_1["volu"]["quad"]
132volu["coil2"] = ret2_2["volu"]["quad"]
133volu["coil3"] = ret2_3["volu"]["quad"]
134volu["coil4"] = ret2_4["volu"]["quad"]
135
136# ------------------------------------------------- #
137# --- simulation region --- #
138# ------------------------------------------------- #
139
140simulation_region = "box"
141
142if ( simulation_region == "box" ):
143 xSim = 2.0
144 ySim = 2.0
145 zSim = 2.0
146
147 x1_sim = [ -xSim, -ySim, -zSim ]
148 x2_sim = [ -xSim, +ySim, -zSim ]
149 x3_sim = [ +xSim, +ySim, -zSim ]
150 x4_sim = [ +xSim, -ySim, -zSim ]
151 delta = [ 0.0, 0.0, 2.0*zSim ]
152 ret3 = qua.generate__quadShape( lc=lc_sim, x1=x1_sim, x2=x2_sim, x3=x3_sim, x4=x4_sim, \
153 extrude_delta=delta, defineVolu=True )
154 volu["air"] = ret3["volu"]["quad"]
155
156elif ( simulation_region == "sphere" ):
157 sph = [ 0.0, 0.0, 0.0, 2.0 ]
158 ret = gmsh.model.occ.addSphere( sph[0], sph[1], sph[2], sph[3] )
159 volu["air"] = ret
160
161
162# ------------------------------------------------- #
163# --- [4] Physical Grouping --- #
164# ------------------------------------------------- #
165
166gmsh.model.occ.removeAllDuplicates()
167
168farBCs = [ 28, 29, 30, 31, 32, 33 ]
169
170gmsh.model.occ.synchronize()
171voluPhys["cMag"] = gmsh.model.addPhysicalGroup( voluDim, [ volu["cMag"] ], tag=301 )
172voluPhys["coil"] = gmsh.model.addPhysicalGroup( voluDim, [ volu["coil1"], volu["coil2"], \
173 volu["coil3"], volu["coil4"] ], tag=302 )
174voluPhys["air"] = gmsh.model.addPhysicalGroup( voluDim, [ volu["air"] ], tag=303 )
175
176surfPhys["far"] = gmsh.model.addPhysicalGroup( surfDim, farBCs, tag=201 )
177
178# ------------------------------------------------- #
179# --- [2] post process --- #
180# ------------------------------------------------- #
181gmsh.model.occ.synchronize()
182gmsh.model.mesh.generate(3)
183gmsh.write( "model.geo_unrolled" )
184gmsh.write( "model.msh" )
185gmsh.finalize()
186
C型電磁石の磁場解析用 Elmer入力ファイル¶
以下にElmer入力ファイルのサンプルを示す.
1! ========================================================= !
2! === C-Shape Magnet and coil === !
3! ========================================================= !
4
5! ------------------------------------------------- !
6! --- [1] Global Simulation Settings --- !
7! ------------------------------------------------- !
8
9CHECK KEYWORDS "Warn"
10
11Header
12 Mesh DB "." "model"
13 Include Path ""
14 Results Directory ""
15End
16
17Simulation
18 coordinate system = "Cartesian"
19 Coordinate Mapping(3) = 1 2 3
20
21 Simulation Type = "Steady State"
22 Steady State Max Iterations = 1
23
24 Solver Input File = "cShape_magnet.sif"
25 Output File = "cShape_magnet.dat"
26 Post File = "cShape_magnet.vtu"
27End
28
29
30Constants
31 Permeability of Vacuum = 1.2566e-06
32End
33
34
35! ------------------------------------------------- !
36! --- [2] Body & Material Settings --- !
37! ------------------------------------------------- !
38
39Body 1
40 Target Bodies(1) = 302
41 Name = "coil"
42
43 Equation = 1
44 Material = 1
45 Body Force = 1
46End
47
48Body 2
49 Target Bodies(1) = 301
50 Name = "core"
51
52 Equation = 2
53 Material = 2
54End
55
56Body 3
57 Target Bodies(1) = 303
58 Name = "air"
59
60 Equation = 2
61 Material = 3
62End
63
64
65Material 1
66 Name = "Cupper"
67 Electric Conductivity = 5.0e7
68 Relative Permittivity = 1.0
69 Relative Permeability = 1.0
70End
71
72Material 2
73 Name = "Iron"
74 Electric Conductivity = 1.0e7
75 Relative Permittivity = 1.0
76 Relative Permeability = 5000
77
78 H-B Curve(38,2) = Real
79 INCLUDE HBcurve.dat
80End
81
82Material 3
83 Name = "Air"
84 Electric Conductivity = 0.0
85 Relative Permittivity = 1.0
86 Relative Permeability = 1.0
87End
88
89
90Component 1
91 Name = "Coil"
92 Coil Type = "test"
93 Master Bodies(1) = 1
94 Desired Coil Current = +1.0e5
95End
96
97! ------------------------------------------------- !
98! --- [3] Equation & Solver Settings --- !
99! ------------------------------------------------- !
100
101Equation 1
102 Name = "MagneticField_in_Coil"
103 Active Solvers(3) = 1 2 3
104End
105
106Equation 2
107 Name = "MagneticField_in_Material"
108 Active Solvers(2) = 2 3
109End
110
111
112Solver 1
113 Equation = "CoilSolver"
114 Procedure = "CoilSolver" "CoilSolver"
115
116 Linear System Solver = "Iterative"
117 Linear System Preconditioning = "ILU1"
118 Linear System Max Iterations = 3000
119 Linear System Convergence Tolerance = 1e-08
120 Linear System Iterative Method = "BiCGStabL"
121 Linear System Residual Output = 20
122 Steady State Convergence Tolerance = 1e-06
123
124 Optimize Bandwidth = True
125 Nonlinear System Consistent Norm = True
126 Coil Closed = Logical True
127 Narrow Interface = Logical False
128
129 Normalize Coil Current = Logical True
130 Save Coil Set = Logical False
131 Save Coil Index = Logical False
132 Calculate Elemental Fields = Logical True
133End
134
135Solver 2
136 Equation = "WhitneySolver"
137 Variable = "AV"
138 Variable Dofs = 1
139 Procedure = "MagnetoDynamics" "WhitneyAVSolver"
140
141 Linear System Solver = "Iterative"
142 Linear System Iterative Method = "BiCGStab"
143 Linear System Max Iterations = 3000
144 Linear System Convergence Tolerance = 1.0e-6
145 Linear System Preconditioning = "None"
146 Linear System Symmetric = True
147
148 Steady State Convergence Tolerance = 1.0e-6
149 Nonlinear System Convergence Tolerance = 1.0e-8
150 Nonlinear System Max Iterations = 100
151 Nonlinear System Newton After Iterations = 3
152 Nonlinear System Newton After Tolerance = 1.0e-8
153 Nonlinear System Relaxation Factor = 0.5
154End
155
156Solver 3
157 Equation = "MGDynamicsCalc"
158 Procedure = "MagnetoDynamics" "MagnetoDynamicsCalcFields"
159 Potential Variable = String "AV"
160
161 Calculate Current Density = Logical True
162 Calculate Magnetic Field Strength = Logical True
163
164 Steady State Convergence Tolerance = 0
165 Linear System Solver = "Iterative"
166 Linear System Preconditioning = None
167 Linear System Residual Output = 0
168 Linear System Max Iterations = 5000
169 Linear System Iterative Method = "CG"
170 Linear System Convergence Tolerance = 1.0e-8
171 Linear System Symmetric = True
172
173 Nonlinear System Consistent Norm = Logical True
174 Discontinuous Bodies = True
175End
176
177
178! ------------------------------------------------- !
179! --- [4] Body Forces / Initial Conditions --- !
180! ------------------------------------------------- !
181
182Body Force 1
183 Name = "CoilCurrentSource"
184 Current Density 1 = Equals "CoilCurrent e 1"
185 Current Density 2 = Equals "CoilCurrent e 2"
186 Current Density 3 = Equals "CoilCurrent e 3"
187End
188
189
190! ------------------------------------------------- !
191! --- [5] Boundary Conditions --- !
192! ------------------------------------------------- !
193
194Boundary Condition 1
195 Name = "Far Boundary"
196 Target Boundaries(1) = 201
197 AV {e} = 0.0
198End
C型電磁石の入力ファイルの要点は以下である.
H-B Curveにより H-B 曲線をデータとして与えている.
Body 1 に付随する component を定義し、無次元量として理想電流 100 (kA) を与えている.
Body Force を定義し、componentが作っている電流を体積力として定義している.
Coil Closed を True としている.
円環コイル電流がつくる磁場の解析結果¶
解析実行結果は以下に示す.以下に電流密度分布と軸方向の磁束密度を示す.
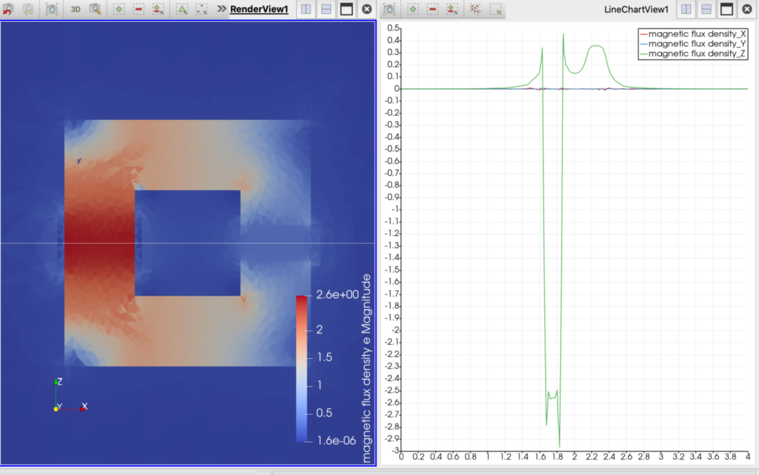
C型電磁石 がギャップ間につくる磁場は、アンペールの法則より、
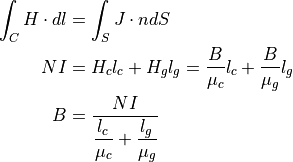
もし、C型電磁石のように鉄芯の透磁率が真空の透磁率に比べて十分大きい場合( 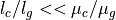 )、磁場は、
)、磁場は、
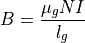
と計算できる.これは、磁気回路において、導線に相当する鉄芯において起磁力降下が生じないことを意味している.つまり、全ての起磁力はギャップ間での磁場の発生のために使われていることになる.上式を用いて、ギャップ間の磁場を計算すると、
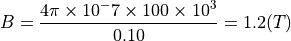
である.
一方、FEMにより磁場解析の結果ではギャップ近辺での磁場は 0.36 (T) であり、1/4程度となっている. これは、定義した H-B 曲線による比透磁率が 100 程度であるため、磁気抵抗が大きく、有限の起磁力降下が鉄芯内で生じたことにより、磁場が小さくなっていると考えられる.
参考例として、以下に、H-B 曲線をコメントアウトし、非透磁率 5000 一定で線形計算した場合の磁場分布を示す.
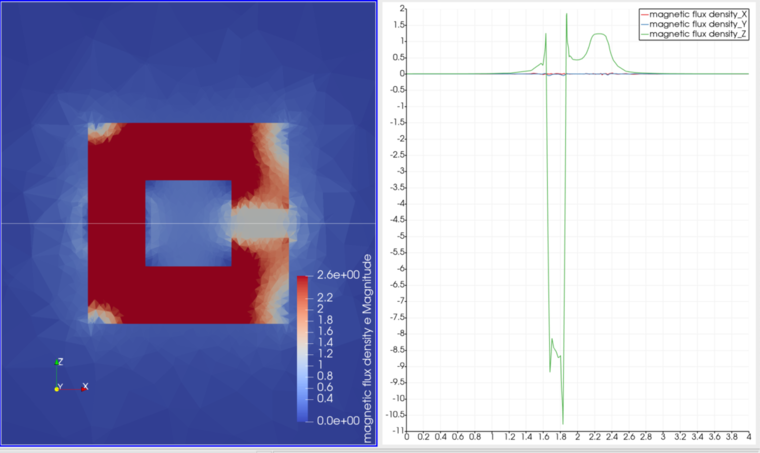
こちらでは、上記の過程が概ね成立し、ギャップ間において、1.2 (T) 磁場強度が得られている.
