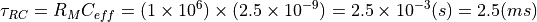二次電子モニタ測定系の等価回路解析 (2)¶
パラメータからみた波形の妥当性¶
項目 |
観測波形 |
回路定数より推定した理論値 |
|---|---|---|
振幅 |
0.8-1.2 |
1.0 |
時定数 |
1.0-2.5 |
|
オフセット |
0.4 |
0.4 |
理論値の計算 (1) (振幅と時定数)¶
入力信号の平均電流値は
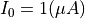 を考える.
を考える.PHITSを用いた出力信号のシミュレーション値(金属板を 200 uA ビームで撃った際の二次電子放出量)
出力信号の波高値としては、ビームデューティ 0.13 %で割って、
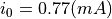 とする.
とする.
入力容量 20 (pF) とケーブル容量 2.5 (nF) の合成キャパシタンスは、ケーブル容量が支配的と考えられるので、ほぼケーブル容量 ( 2.5 (nF) )としてよい.
ビームパルスの出力時間 (
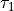 )は、3 (us) とする.
)は、3 (us) とする.式中の
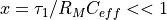 であるため、 Taylor 展開より
であるため、 Taylor 展開より 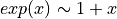 が使用できる.
が使用できる.ここで、
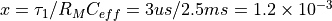 である.
である.
理論値の計算 (2) (オフセット)¶
オフセットは、繰り返し周波数を上昇させたときのみ、発生.
300 pps での典型値は 0.4 (V) 程度.
インパルス応答ではなく、周期的なパルス列に対する応答を考えれば、expが有限時間内に減衰しきらない分だけオフセットが生じる.
インパルス列に対する応答の式¶
![v_{pulse} (t) =
\begin{cases}
R i_0 \left[ 1 - e^{ -\dfrac{t}{RC} } \right] \ \ &( t < \tau_1 ) \\
R i_0 \left[ 1 - e^{ -\dfrac{\tau_1}{RC} } \right] e^{ \dfrac{t-\tau_1}{RC} } \ \ &( t > \tau_1 )
\end{cases}](../../../_images/math/5ac0bcf03681749e68965a3c5b0ddf0a14c36738.png)
上記の、t=0 まわりに着目したインパルス応答が、 k=1,2,3,...,n のパルス列が過去に入っていた.これは、時刻、 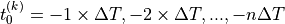 に発火したパルスである.発火の周期が
に発火したパルスである.発火の周期が 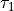 より長いとして2式に着目し、統一した時間の関数として各インパルス応答を記述すると、
より長いとして2式に着目し、統一した時間の関数として各インパルス応答を記述すると、
![v_{pulse} (t-t_0^{(k)}) &= R i_0 \left[ 1 - e^{ -\dfrac{\tau_1}{RC} } \right] e^{ \dfrac{t-t_0^{(k)}-\tau_1}{RC} } \\
&= R i_0 \left[ 1 - e^{ -\dfrac{\tau_1}{RC} } \right] e^{ \dfrac{t- k\Delta T-\tau_1}{RC} } \\
&= v_{pulse}(t) e ^{ - \dfrac{k \Delta T}{RC} }](../../../_images/math/bd363c7ca979ced2c2cc1bb3ba611e4696a0d093.png)
k=1,2,...,n まで足し合わせて、 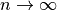 とすれば、
とすれば、
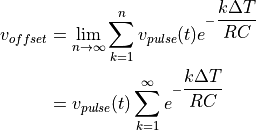
ここで、初項 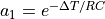 , 公比
, 公比 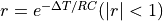 の無限等比級数の和は、
の無限等比級数の和は、
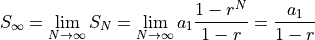
であるから、
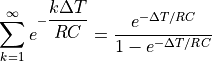
より、 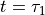 における オフセットは
における オフセットは
![v_{offset} &= v_{pulse}(\tau_1) \dfrac{ e^{- \Delta T / RC } }{ 1 - e^{- \Delta T / RC } } \\
&= R i_0 \left[ 1 - e^{ - \dfrac{\tau_1}{RC}} \right] \dfrac{ e^{- \Delta T / RC } }{ 1 - e^{- \Delta T / RC } }](../../../_images/math/bb8c258bc59182231e80aaa1722ab1d67399fa0d.png)
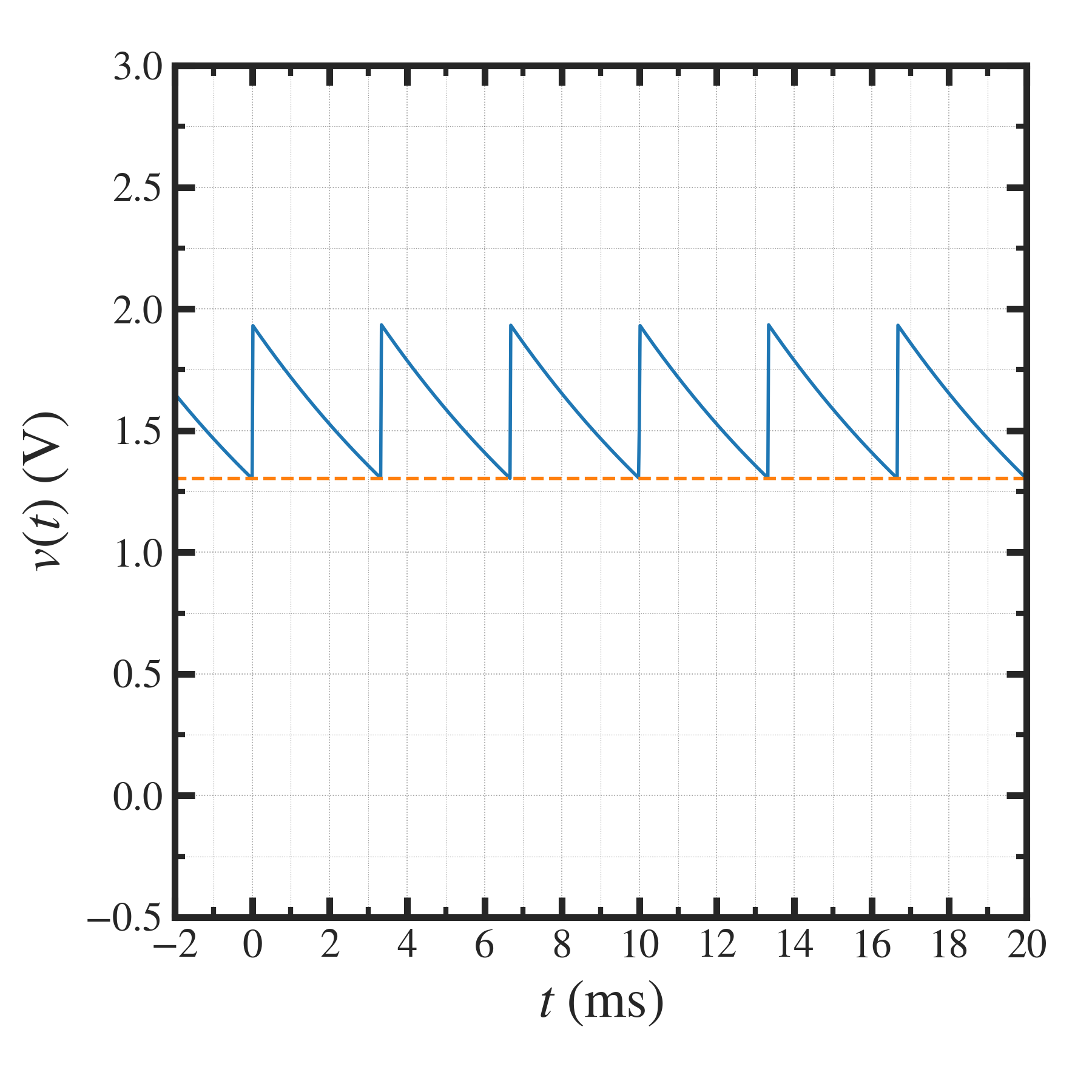
例えば、 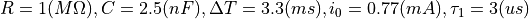 を使用すれば、
を使用すれば、
![v_{offset} &= 10^6 \times 0.77 \times 10^{-3} \left[ 1 - e^{ - \dfrac{ 3 \times 10^{-6} }{ 2.5 \times 10^{-3} } } \right] \dfrac{ e^{- 3.3 / 2.5 } }{ 1 - e^{- 3.3 / 2.5 } } \\
&= 0.92 \times 0.365 \\
&= 0.335 (V)](../../../_images/math/7a656e50403a7f16048245fdb3788944af0b2781.png)
となる.これは、実験的に観測した値 0.4 (V) を説明できると考えられる.
数値的に模擬¶
出力信号を、解析的にではなく、数値的に模擬してみた.
import os, sys
import numpy as np
# ========================================================= #
# === calculate__past_kth_signal === #
# ========================================================= #
def calculate__past_kth_signal( time, tau1, tau2, tauRC, RM, i0, kth ):
ret = np.copy( time ) * 0.0
t1 = 0.0 - kth*tau2
t2 = tau1 - kth*tau2
sig1 = time * 0.0
sig2 = RM*i0 * ( 1.0 - np.exp( (-1.0)*(time-t1)/tauRC ) )
sig3 = RM*i0 * ( 1.0 - np.exp( (-1.0)*tau1/tauRC ) ) \
* np.exp( (-1.0)*tau2/tauRC * kth ) \
* np.exp( (-1.0)*(time)/tauRC )
ret1 = np.where( time< t1 , sig1, 0.0 )
ret2 = np.where( (time>=t1)&(time<t2), sig2, 0.0 )
ret3 = np.where( time>=t2 , sig3, 0.0 )
ret = ret1 + ret2 + ret3
return( ret )
# ========================================================= #
# === SEEmonitor_multiPulseSignal.py === #
# ========================================================= #
def SEEmonitor_multiPulseSignal():
ms = 1.e-3
t_, v_, o_ = 0, 1, 2
# ------------------------------------------------- #
# --- [1] def parameters --- #
# ------------------------------------------------- #
CC = 8.4e-9
RC = 2.5
CM = 20.0e-12
RM = 1.0e+6
tau1 = 3.0e-6
tau2 = 3.333e-3
tau3 = 20.0e-3
nT1 = 11
nT2 = 51
I_SEE_ave = 0.97e-6/200.0 * 210.0 * 1.57
tau_beam = 3.0e-6
f_Repeat = 300.0
duty = tau_beam * f_Repeat
I_SEE_pulse = I_SEE_ave / duty
i0 = I_SEE_pulse
print( " i0 == {}".format( i0 ) )
# ------------------------------------------------- #
# --- [2] calculation --- #
# ------------------------------------------------- #
tauRC = RM * ( CC + CM )
time = np.linspace( -1.0*tau3, 1.0*tau3, 2001 )
kth_list = np.arange( -200, 20 )
vt = np.copy( time ) * 0.0
for kth in kth_list:
vt_iter = calculate__past_kth_signal( time, tau1, tau2, tauRC, RM, i0, kth )
vt += vt_iter
a0 = RM*i0 * ( 1.0-np.exp( -1.0*tau1/tauRC ) )
r = np.exp( -1.0*tau2/tauRC )
S_inf = a0 * r/( 1.0-r )
v_ofs = np.zeros_like( time ) + S_inf
time = np.reshape( time, [-1,1] )
vt = np.reshape( vt, [-1,1] )
vo = np.reshape( v_ofs, [-1,1] )
Data = np.concatenate( [time,vt,vo], axis=1 )
# ------------------------------------------------- #
# --- [3] save data in a file --- #
# ------------------------------------------------- #
import nkUtilities.save__pointFile as spf
outFile = "dat/SEEmonitor__multiPulseSignal.dat"
spf.save__pointFile( outFile=outFile, Data=Data, names=["t","v(t)", "i(t)", "q(t)"] )
# ------------------------------------------------- #
# --- [4] display in a file --- #
# ------------------------------------------------- #
import nkUtilities.plot1D as pl1
import nkUtilities.load__config as lcf
import nkUtilities.configSettings as cfs
x_,y_ = 0, 1
pngFile = "png/SEEmonitor__multiPulseSignal.png"
config = lcf.load__config()
config = cfs.configSettings( configType="plot.def", config=config )
config["FigSize"] = (4.5,4.5)
config["plt_position"] = [ 0.16, 0.16, 0.94, 0.94 ]
config["plt_xAutoRange"] = False
config["plt_yAutoRange"] = False
config["plt_xRange"] = [ -2.0, +20.0 ]
config["plt_yRange"] = [ -0.5, +3.0 ]
config["xMajor_Nticks"] = 12
config["yMajor_Nticks"] = 8
config["plt_marker"] = "none"
config["plt_markersize"] = 2.0
config["plt_linestyle"] = "-"
config["plt_linewidth"] = 1.0
config["xTitle"] = "$t \ \mathrm{(ms)}$"
config["yTitle"] = "$v(t) \ \mathrm{(V)}$"
fig = pl1.plot1D( config=config, pngFile=pngFile )
fig.add__plot( xAxis=Data[:,t_]/ms, yAxis=Data[:,v_] )
fig.add__plot( xAxis=Data[:,t_]/ms, yAxis=Data[:,o_], linestyle="--" )
fig.set__axis()
fig.save__figure()
return()
# ========================================================= #
# === Execution of Pragram === #
# ========================================================= #
if ( __name__=="__main__" ):
SEEmonitor_multiPulseSignal()
計算過程¶
出力信号の結論¶
上記、回路定数から予想される出力信号と、同等な信号が実験により得られていることから、検討した等価回路モデルが良く実験を表していると考えられる.
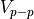 (V)
(V)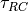 (ms)
(ms)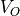 (V)
(V)![V_{p-p} &= i_0 R_M \left[ 1 - e^{ - \dfrac{\tau_1} {R_M C_{eff}} } \right] \\
& \sim i_0 R_M \dfrac{\tau_1} {R_M C_{eff}} \\
& \sim ( 0.77 \times 10^{-3} ) \times ( 1 \times 10^6 ) \times (1.2 \times 10^{-3}) \\
& \sim 0.92 (V)](../../../_images/math/0c967aae7787e85fa90578b33efe8f8912d0c567.png)