二次電子モニタ測定系の等価回路解析 (1)¶
背景¶
金属片を用いた二次電子モニタを作成
電流源として動作する二次電子モニタに対し、同軸ケーブルでオシロスコープへ接続した場合の観測波形について考えたい.
同軸ケーブル・オシロスコープの等価回路を考えて、観測波形が説明したい.
ポイント¶
等価回路から導出される一般解は、得られる波形を説明できるか?
等価回路の回路定数を用いて、得られる波形を説明できるか?
振幅
時間構造 ( 周期、時定数 )
オフセット
信号波形(解析値)¶
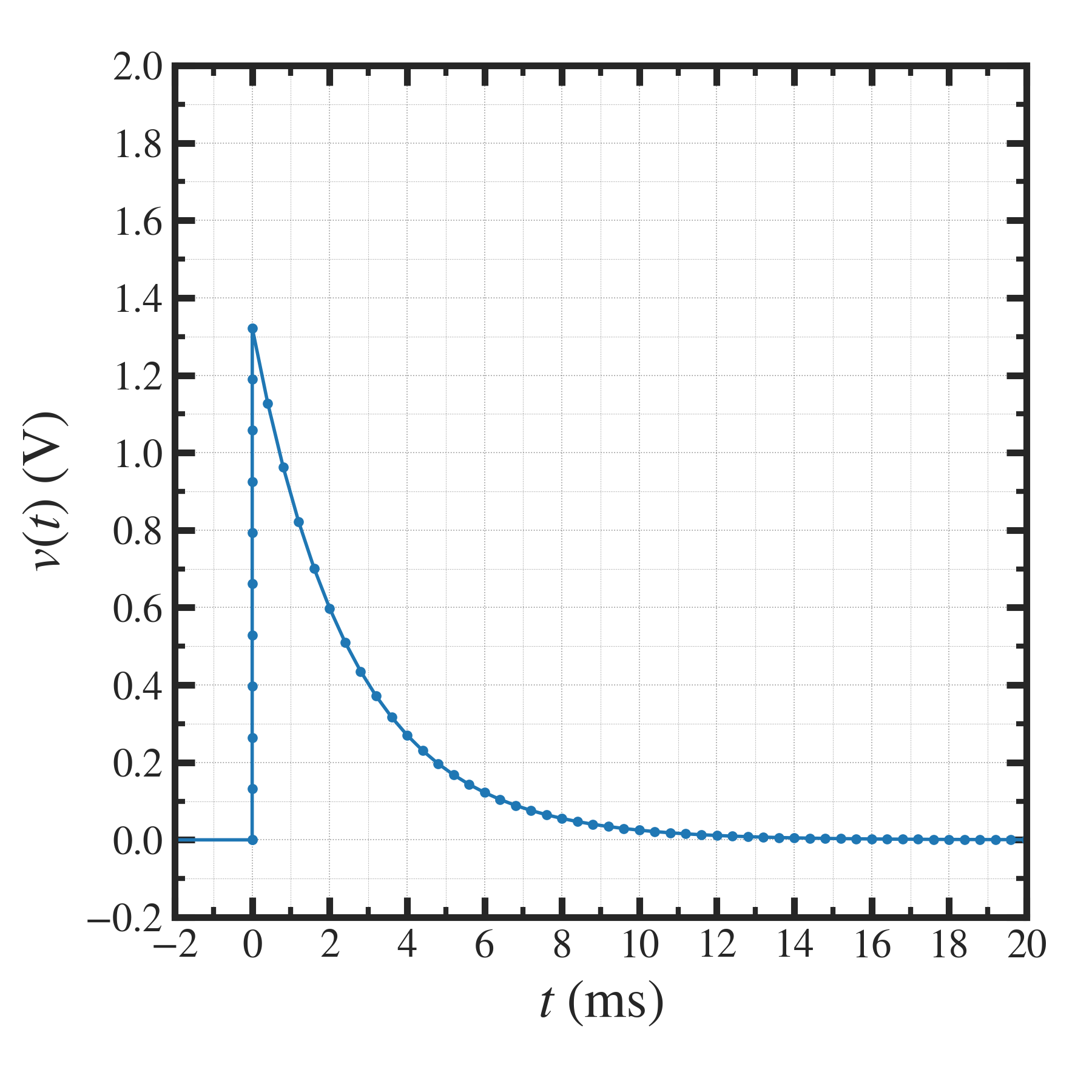
理論信号波形プロット (一般解)¶
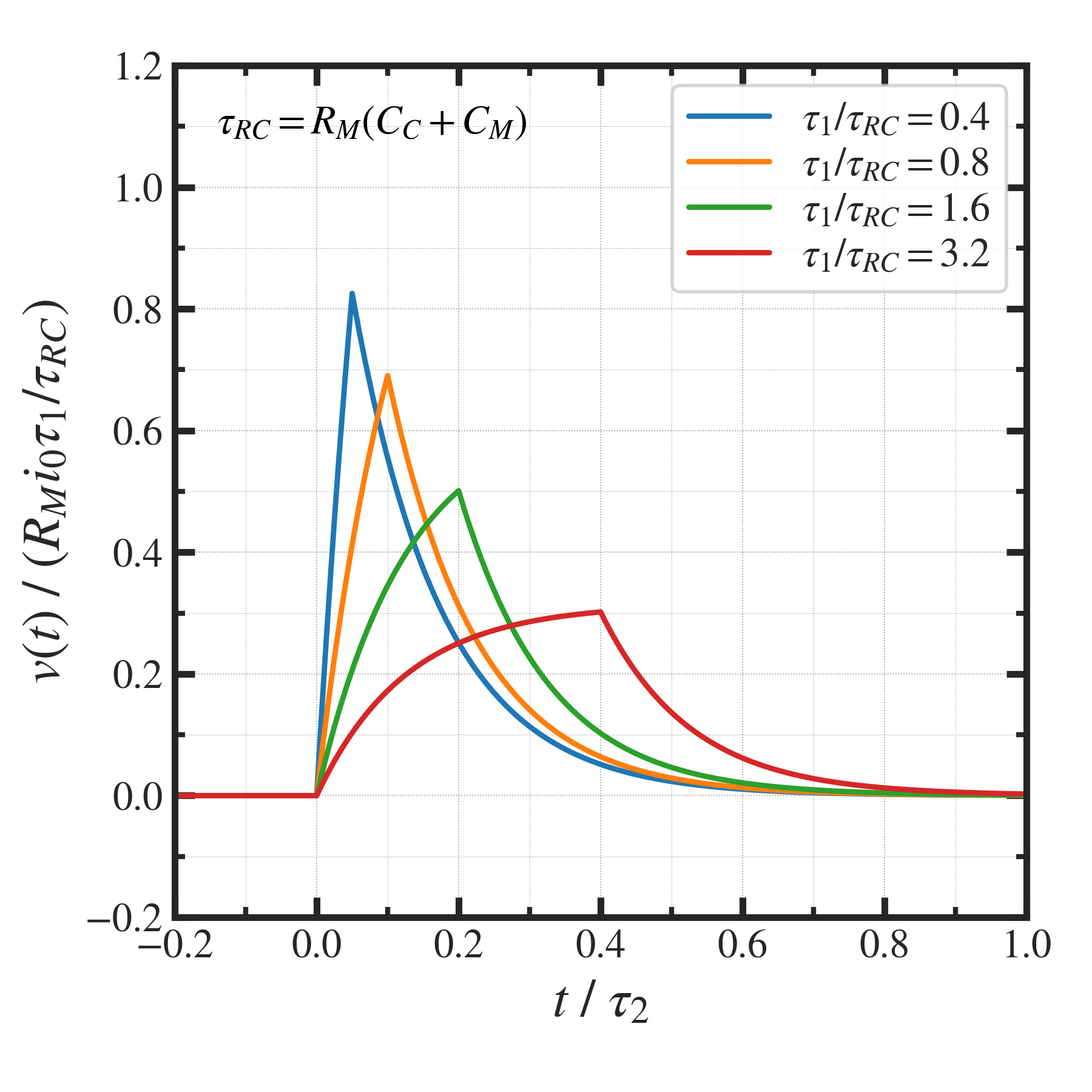
ビームパルス(
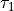 )が、回路の時定数(
)が、回路の時定数( 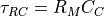 )よりも、十分、短時間であれば、パルス状に瞬時に立ち上がり、そのあと、減衰していく波形となる.(実際に観測されたデータはそのような波形)
)よりも、十分、短時間であれば、パルス状に瞬時に立ち上がり、そのあと、減衰していく波形となる.(実際に観測されたデータはそのような波形)
図示プログラム¶
import numpy as np
# ========================================================= #
# === SEEmonitor_model_graph.py === #
# ========================================================= #
def SEEmonitor_model_graph():
ms = 1.e-3
t_, v_, i_, q_ = 0, 1, 2, 3
# ------------------------------------------------- #
# --- [1] def parameters --- #
# ------------------------------------------------- #
CC = 8.8e-9
RC = 2.5
CM = 20.0e-12
RM = 1.0e+6
tau1 = 3.0e-6
tau2 = 3.3e-3
tau3 = 20.0e-3
nT1 = 11
nT2 = 51
I_SEE_ave = 2.0e-6
tau_beam = 3.0e-6
f_Repeat = 300.0
duty = tau_beam * f_Repeat
I_SEE_pulse = I_SEE_ave / duty
i0 = I_SEE_pulse
print( " i0 == {}".format( i0 ) )
# ------------------------------------------------- #
# --- [2] calculation --- #
# ------------------------------------------------- #
tauRC = RM * ( CC + CM )
t_pre = np.array( [-1e10, 0.0] )
t1 = ( np.linspace( 0.0, tau1 , nT1 ) )[0:]
# t2 = ( np.linspace( tau1, tau1+tau2, nT2 ) )[1:]
t2 = ( np.linspace( tau1, tau3, nT2 ) )[1:]
qchg = tauRC * i0 * ( 1.0 - np.exp( - tau1 / tauRC ) )
v1 = RM * i0 * ( 1.0 - np.exp( - t1 / tauRC ) )
i1 = i0 * ( np.exp( - t1 / tauRC ) )
q1 = tauRC * i0 * ( 1.0 - np.exp( - t1 / tauRC ) )
v2 = qchg / (CC+CM) * ( np.exp( - ( t2 - tau1 ) / tauRC ) )
i2 = qchg / tauRC * ( np.exp( - ( t2 - tau1 ) / tauRC ) )
q2 = qchg * ( np.exp( - ( t2 - tau1 ) / tauRC ) )
v_pre = np.array( [0.0,0.0] )
i_pre = np.array( [0.0,0.0] )
q_pre = np.array( [0.0,0.0] )
time = np.reshape( np.concatenate( [t_pre,t1,t2] ), [-1,1] )
vt = np.reshape( np.concatenate( [v_pre,v1,v2] ), [-1,1] )
it = np.reshape( np.concatenate( [i_pre,i1,i2] ), [-1,1] )
qt = np.reshape( np.concatenate( [q_pre,q1,q2] ), [-1,1] )
Data = np.concatenate( [time,vt,it,qt], axis=1 )
print( Data.shape )
# ------------------------------------------------- #
# --- [3] save data in a file --- #
# ------------------------------------------------- #
import nkUtilities.save__pointFile as spf
outFile = "dat/SEEmonitor_model_graph.dat"
spf.save__pointFile( outFile=outFile, Data=Data, names=["t","v(t)", "i(t)", "q(t)"] )
# ------------------------------------------------- #
# --- [4] display in a file --- #
# ------------------------------------------------- #
import nkUtilities.plot1D as pl1
import nkUtilities.load__config as lcf
import nkUtilities.configSettings as cfs
x_,y_ = 0, 1
pngFile = "png/SEEmonitor_model_graph_v_vs_time.png"
config = lcf.load__config()
config = cfs.configSettings( configType="plot.def", config=config )
config["FigSize"] = (4.5,4.5)
config["plt_position"] = [ 0.16, 0.16, 0.94, 0.94 ]
config["plt_xAutoRange"] = False
config["plt_yAutoRange"] = False
config["plt_xRange"] = [ -2.0, +20.0 ]
config["plt_yRange"] = [ -0.2, +2.0 ]
config["xMajor_Nticks"] = 12
config["yMajor_Nticks"] = 12
config["plt_marker"] = "o"
config["plt_markersize"] = 2.0
config["plt_linestyle"] = "-"
config["plt_linewidth"] = 1.0
config["xTitle"] = "$t \ \mathrm{(ms)}$"
config["yTitle"] = "$v(t) \ \mathrm{(V)}$"
fig = pl1.plot1D( config=config, pngFile=pngFile )
fig.add__plot( xAxis=Data[:,t_]/ms, yAxis=Data[:,v_] )
fig.set__axis()
fig.save__figure()
return()
# ========================================================= #
# === Execution of Pragram === #
# ========================================================= #
if ( __name__=="__main__" ):
SEEmonitor_model_graph()
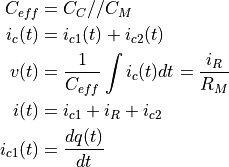
![v(t) &= R_M i_0 \left[ 1 - e^{ - \dfrac{t} {R_M C_{eff}} } \right] \\
i_{c}(t) &= i_0 e^{ - \dfrac{t} {R_M C_{eff}} } \\
q(t) &= R_M C_{eff} i_0 \left[ 1 - e^{ - \dfrac{t} {R_M C_{eff}} } \right] \\](../../../_images/math/4cf18bb92557a68486c05dba6ce24f3bc46a79d2.png)
![v(t) &= R_M i_0 \left[ 1 - e^{ - \dfrac{\tau_1 }{ R_M C_{eff} } } \right] e^{ - \dfrac{t-\tau_1} {R_M C_{eff}} } \\
i_{c}(t) &= i_0 \left[ 1 - e^{ - \dfrac{\tau_1 }{ R_M C_{eff} } } \right] e^{ - \dfrac{t-\tau_1} {R_M C_{eff}} } \\
q(t) &= R_M C_{eff} i_0 \left[ 1 - e^{ - \dfrac{\tau_1 }{ R_M C_{eff} } } \right] e^{ - \dfrac{t-\tau_1} {R_M C_{eff}} } \\](../../../_images/math/f830fcf718a7167f79f8a1eb3815815b779e02a1.png)