画像処理の座標系について¶

アフィン変換について¶

画像処理の最も基本的変換は、アフィン変換（Affine Conversion）である．
- アフィン変換は、平行移動、拡大縮小、回転、剪断の４要素からなる線形変換である．
- デカルト座標系に対して、拡大縮小、回転、剪断の３変換は、線形変換 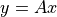$y=Ax$ にて記述が可能．
- 平行移動については、定数項の和で記載が可能．
座標系をそのまま用いた場合の画像変換の、各変形は以下である．
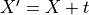- 平行移動：定数項の加減算 ( $X^{\prime} = X + t$ )
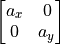- 拡大縮小：対角行列倍 ( $\begin{bmatrix} a_x & 0 \\ 0 & a_y \end{bmatrix}$ )
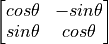- 回転：回転行列倍 ( $\begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix}$ )
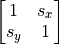- 剪断：シア行列倍 ( $\begin{bmatrix} 1 & s_x \\ s_y & 1 \end{bmatrix}$ )

N次元の座標系を1次元拡張したN+1次元の座標系に変換し、これに対して線形変換することで、N次元空間での平行移動が記述可能である．
- この際に使用する N+1次元の座標空間を同次座標系と呼ぶ．
- 同次座標系は、例えば、[x,y,z]に対して、１次元座標空間を追加した [x,y,z,w] などとして記載されるが、w の値としては何を用いてもよい．よって、w=1とした [x,y,z,1]を同次座標系として用いることが通例である．

平行移動は例えば、次のように記述できる．

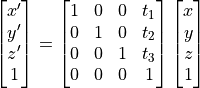
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & t_1 \\ 0 & 1 & 0 & t_2 \\ 0 & 0 & 1 & t_3 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}$

剛体変換は、回転、及び、平行移動からなる座標変換である．
- 剛体変換は変換前後で体積が保存する．
- 拡大縮小や剪断を含まないアフィン変換である．
剛体変換は、同次座標系を用いて、以下のように記述できる．

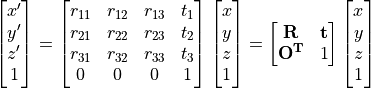
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \\ z^{\prime} \\ 1 \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13} & t_1 \\ r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \bf{R} & \bf{t} \\ \bf{O}^T & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}$

カメラを用いて、透視投影して３次元物体を２次元画像へ写像した際の変換を以下に記す．

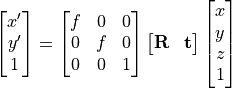
$\begin{bmatrix} x^{\prime} \\ y^{\prime} \\ 1 \end{bmatrix} = \begin{bmatrix} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \bf{R} & \bf{t} \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}$