割線法 ( secant solver )

割線法は， Newton-Raphson 法における微分評価を数値微分とした求解アルゴリズムである．

割線法のアルゴリズム

方程式 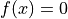f(x)=0 を解く割線法のアルゴリズムは Newton-Raphson 法とほぼ同様であり，微分評価の手法が異なる．

  1. n 回目における座標 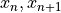x_n, x_{n+1} における関数値 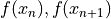f(x_n), f(x_{n+1}) を求める．

  2. 次のステップでの座標 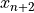x_{n+2} を次式から評価する

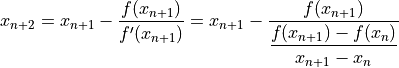
x_{n+2} = x_{n+1} - \dfrac{ f( x_{n+1} ) }{ f^{\prime}( x_{n+1} ) } = x_{n+1} - \dfrac{ f( x_{n+1} ) }{ \dfrac{ f( x_{n+1} ) - f( x_n ) }{ x_{n+1} - x_n } }

  1. 得られた数値解が許容誤差より低ければ ( 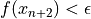f(x_{n+2}) < \epsilon )，解探索を終了し，許容誤差より大きければステップ1に戻って，解をもう１ステップ進める．

割線法の特徴

長所

  • 解くべき関数のみを与えれば良い． ( Newton-Raphson 法では，解析的な関数とその解析微分が必要 )

  • 一般的に，二分法よりも収束が速い ( 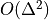O(\Delta^2) の収束 )

短所

  • 収束の安定性が保証されていない．

サンプルコード

サンプルコードを以下に示す．

main.f90
 1program main
 2  use secantSlvMod
 3  implicit none
 4  double precision, parameter :: xMin    = 0.d0
 5  double precision, parameter :: xMax    = 4.d0
 6  integer         , parameter :: nData   = 101
 7  integer         , parameter :: lun     = 50
 8  integer         , parameter :: iterMax = 100
 9  double precision, parameter :: crit    = 1.d-12
10  integer                     :: i
11  double precision            :: xi(nData), yi(nData)
12  double precision            :: x1, x2
13  
14  ! ------------------------------------------------------ !
15  ! --- [1] solve by secant Method                     --- !
16  ! ------------------------------------------------------ !
17  x1 = 0.d0
18  x2 = 1.d0
19  call secantMethod( x1, x2, iterMax, crit )
20  write(6,*) "answer   :: x1 == ", x1
21  write(6,*) "residual :: x2 == ", x2
22  write(6,*) "y1 - theory    == ", analyticFunc( x1 )
23  write(6,*) "theory L.H.S.  == ", sin(x1) + cos(x1) 
24  write(6,*) "theory R.H.S.  == ", 0.707d0
25  
26  return
27end program main
secantSlvMod.f90
 1module secantSlvMod
 2contains
 3
 4  
 5  ! ====================================================== !
 6  ! === analyticFunc                                   === !
 7  ! ====================================================== !
 8  function analyticFunc( xv )
 9    implicit none
10    double precision, intent(in)  :: xv
11    double precision              :: analyticFunc
12    
13    analyticFunc = sin( xv ) + cos( xv ) - 0.707d0
14    return
15  end function analyticFunc
16  
17  
18  ! ====================================================== !
19  ! === secantMethod                                   === !
20  ! ====================================================== !
21  subroutine secantMethod( x1, x2, iterMax, crit )
22    implicit none
23    integer         , intent(in)    :: iterMax
24    double precision, intent(in)    :: crit
25    double precision, intent(inout) :: x1, x2
26    integer                         :: iter
27    double precision                :: y1, y2, fpInv
28    
29    ! ------------------------------------------------------ !
30    ! --- [1] Solve Main Iteration                       --- !
31    ! ------------------------------------------------------ !
32    y1 = analyticFunc( x1 )
33    y2 = analyticFunc( x2 )
34    do iter=1, iterMax
35       fpInv = ( x2 - x1 ) / ( y2 - y1 )
36       x1    = x2
37       y1    = y2
38       x2    = x2 - y2 * fpInv
39       y2    = analyticFunc( x2 )
40       if ( abs(y2).lt.crit ) exit
41    enddo
42    ! ------------------------------------------------------ !
43    ! --- [2] return variables                           --- !
44    ! ------------------------------------------------------ !
45    x1 = x2
46    x2 = y2
47    
48    return
49  end subroutine secantMethod
50  
51end module secantSlvMod

実行結果例

実行結果例を以下に示す．

kent@euler ~/fortran/secantSolver $ ./main
answer   :: x1 ==  -0.26188657207873522
residual :: x2 ==   -1.1102230246251565E-016
y1 - theory    ==   -1.1102230246251565E-016
theory L.H.S.  ==   0.70699999999999985
theory R.H.S.  ==   0.70699999999999996