二分法 ( Bisection Solver )¶
安定に解ける求解アルゴリズムの一つ.解を含む有限の区間を指定することができれば,その両端を解へと漸近させていくことで解を求めることができることを利用する. 二分法のアルゴリズムは以下の通り.
方程式
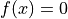 の初期解として,解
の初期解として,解 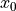 を含む有限の区間
を含む有限の区間 ![[a,b]](../../../_images/math/b17897287b23d96473a85f41eeb859a16830b679.png) の両端座標を与える.ただし,
の両端座標を与える.ただし, 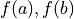 は解
は解 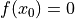 を挟んで,異なる符号を有するものとする.
を挟んで,異なる符号を有するものとする.解空間の両端の平均値
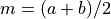 を計算する.
を計算する.解空間両端 a, b のうち,m と関数
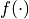 の符号が同じであればをmと置き換える.
の符号が同じであればをmと置き換える.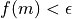 (
(  :許容誤差 ) であれば,解探索を終了する.条件を満たさない場合, 1-4 を再度繰り返す.
:許容誤差 ) であれば,解探索を終了する.条件を満たさない場合, 1-4 を再度繰り返す.
二分法の特徴¶
長所
解の存在が保証されており, 安定に解くことができる .
短所
解の 収束が遅い .
推測値として与える 初期解 の設定が比較的難しい.解の存在が保証され,およその座標を特定でき,正負両方向から挟んだ初期解を与える必要がある.
サンプルコード¶
以下に 二分法のサンプルコードを示す.
メインルーチン.初期解を与えて二分法ルーチンを呼び,結果を表示する.
main.f90¶
1program main
2 use bisectionMod
3 implicit none
4 double precision, parameter :: xMin = 0.d0
5 double precision, parameter :: xMax = 4.d0
6 integer , parameter :: nData = 101
7 integer , parameter :: lun = 50
8 integer , parameter :: iterMax = 100
9 double precision, parameter :: crit = 1.d-12
10 integer :: i
11 double precision :: xi(nData), yi(nData)
12 double precision :: x1, x2
13
14 ! ------------------------------------------------------ !
15 ! --- [1] solve by bisection Method --- !
16 ! ------------------------------------------------------ !
17 x1 = 0.d0
18 x2 = 1.d0
19 call bisectionMethod( x1, x2, iterMax, crit )
20 write(6,*) x1, x2, analyticFunc( x1 ), sin(x1)
21
22 return
23end program main
二分法求解ルーチン. analyticFunc が求解すべき関数 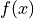 を返却する解析関数.
サブルーチン bisectionMethod は,
を返却する解析関数.
サブルーチン bisectionMethod は,
bisectionMod.f90¶
1module bisectionMod
2contains
3
4
5 ! ====================================================== !
6 ! === analyticFunc === !
7 ! ====================================================== !
8 function analyticFunc( xv )
9 implicit none
10 double precision, intent(in) :: xv
11 double precision :: analyticFunc
12
13 analyticFunc = sin( xv ) - 0.707d0
14 return
15 end function analyticFunc
16
17
18 ! ====================================================== !
19 ! === bisectionMethod === !
20 ! ====================================================== !
21 subroutine bisectionMethod( x1, x2, iterMax, crit )
22 implicit none
23 integer , intent(in) :: iterMax
24 double precision, intent(in) :: crit
25 double precision, intent(inout) :: x1, x2
26 integer :: iter
27 double precision :: xmid, ymid
28 double precision :: sign1, sign2, signm
29
30 ! ------------------------------------------------------ !
31 ! --- [1] sign1 / sign2 --- !
32 ! ------------------------------------------------------ !
33 sign1 = sign( 1.d0, analyticFunc( x1 ) )
34 sign2 = sign( 1.d0, analyticFunc( x2 ) )
35 if ( sign1.eq.sign2 ) then
36 write(6,*) '[bisectionMethod] x1 & x2 :: 2 variables have same sign.'
37 stop
38 endif
39 ! ------------------------------------------------------ !
40 ! --- [2] Solve Main Iteration --- !
41 ! ------------------------------------------------------ !
42 do iter=1, iterMax
43 xmid = 0.5d0 * ( x1 + x2 )
44 ymid = analyticFunc( xmid )
45 signm = sign( 1.d0, ymid )
46 if ( signm.eq.sign1 ) then
47 x1 = xmid
48 else if ( signm.eq.sign2 ) then
49 x2 = xmid
50 endif
51 if ( abs(ymid).lt.crit ) exit
52 enddo
53 ! ------------------------------------------------------ !
54 ! --- [3] return variables --- !
55 ! ------------------------------------------------------ !
56 x1 = xmid
57 x2 = ymid
58
59 return
60 end subroutine bisectionMethod
61
62
63end module bisectionMod
実行例¶
上記サンプルコードの実行例を示す.
解くべき方程式は, 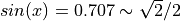 とした.
有限の桁数で打ち切っているが,解は
とした.
有限の桁数で打ち切っているが,解は 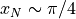 となるはずである.
となるはずである.
kent@euler ~/fortran/bisectionSolver $ ./main
0.78524716339597944 5.8453242246514492E-013 5.8453242246514492E-013 0.70700000000058449
左から, 得られた解と数値的残差 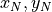 ,解くべき方程式の理論残差値と左辺値
,解くべき方程式の理論残差値と左辺値 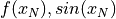 を示している.解は予想される値に十分近い値を示している. (ここでは,右辺を適当に0.707としている.)
を示している.解は予想される値に十分近い値を示している. (ここでは,右辺を適当に0.707としている.)
