ガウスの消去法 ( Gauss Elimination )¶
ガウス ( Gauss ) の消去法 ( Gauss Elimination )は、連立一次方程式の解法の一種である． Gauss-Jordan 法と数学的に同値な手法なので、同一の手法として取り扱われることもあるが、 Numerical Recipes in F77 では別節立てで紹介されており、本解説もこれに倣うことにする． ここでは、
全ての単位行列化を 行基本変形 により担う手法を、 Gauss-Jordan 法
上三角行列化に 前進消去 、単位行列化に 後退代入 を用いる手法を Gauss の消去法
と呼ぶことにする．前進消去・後退代入は、行基本変形によって表現でき、数学的には同値な手法である．一方、同値な操作ではあるが、後退代入によって、 Gauss の消去法は Gauss-Jordan 法に比較して、計算量を定数倍程度節約できる．そのため、ここではアルゴリズムとして、別個のアルゴリズムであると考えることにする．
Gauss の消去法のアルゴリズム¶
Gauss の消去法にも pivoting ( ピボット選択 ) の 種類によって、
部分 pivoting ( full pivoting 行・列、いづれかの方向で pivot 探索する )
完全 pivoting ( full pivoting 行列両方向同時に pivot 探索する )
の2つがある．ここでは、部分 pivoting のアルゴリズムを例として、以下に流れを示す．
行列 A を 行列 U へコピーし、連立一次方程式の解を求める場合は右辺ベクトル、逆行列を求める場合は、右辺単位行列を用意する．
i=1,2,3,...,n 行目に対して、以下の操作を繰り返す． ( 前進消去 )
i行目の対角要素
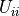を 
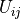( j=i,i+1,...,n ) のうち、最大の値をとるものとして探索する．探索後、初期の行と異なっていれば、2つの行を交換する．i 行目を
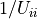倍して、対角要素を 1 とする．i行目以外の全ての j=i~n 行目に対して、 i 列目要素を 0 とする．つまり、i 行目を
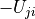倍して、j 行目へ加算する．
i=nからi=1に向けて、上三角行列Uの非対角要素をゼロにする．（ 後退代入 ）
i 行目の対角要素を、以下の式により求める．
![x_i = \dfrac{1}{U_{ii}} \left[ b_i - \sum^n_{j=i+1} U_{ij} x_j \right]](../../../_images/math/f0e07d8ea75c2208715924d30af2f8e7e96769e9.png)
Gauss の消去法のサンプルコード¶
Gauss の消去法のサンプルコードについて、以下に示す．
main.f90¶
1! ====================================================== !
2! === Gauss Elimination Example === !
3! ====================================================== !
4program main
5 use gaussElimMod, only : gaussElimin
6 implicit none
7 integer , parameter :: nSize = 3
8 character(100) , parameter :: FileName = 'dat/eq.inp'
9 double precision, allocatable :: Amat(:,:), bvec(:), xvec(:), res(:)
10 integer :: i, j
11 double precision :: avg, std
12
13 ! ------------------------------------- !
14 ! --- [1] Data Load --- !
15 ! ------------------------------------- !
16 ! -- [1-1] Load from file -- !
17 allocate( Amat(nSize,nSize), bvec(nSize), xvec(nSize) )
18 open(50,file=trim(FileName),status='old',form='formatted')
19 do i=1, nSize
20 read(50,*) Amat(i,:), bvec(i)
21 enddo
22 close(50)
23 ! -- [1-2] input comfirmation -- !
24 write(6,*) 'input matrix | L.H.S. vector'
25 do i=1, nSize
26 write(6,*) Amat(i,:), '|', bvec(i)
27 enddo
28 write(6,*)
29
30 ! ------------------------------------- !
31 ! --- [2] Gauss Elimination --- !
32 ! ------------------------------------- !
33 call gaussElimin( Amat, xvec, bvec, nSize )
34
35 ! ------------------------------------- !
36 ! --- [3] Answer Check --- !
37 ! ------------------------------------- !
38 ! -- [3-1] calculate residual -- !
39 allocate( res(nSize) )
40 do i=1, nSize
41 res(i) = 0.d0
42 do j=1, nSize
43 res(i) = res(i) + Amat(i,j) * xvec(j)
44 enddo
45 enddo
46 res(:) = bvec(:) - res(:)
47 ! -- [3-2] output answer/residual -- !
48 write(6,*) 'answer :: x | residual '
49 do i=1, nSize
50 write(6,*) xvec(i), ' | ', res(i)
51 enddo
52 ! -- [3-3] statistical values -- !
53 avg = 0.d0
54 std = 0.d0
55 do i=1, nSize
56 avg = avg + res(i)
57 std = std + res(i)**2
58 enddo
59 avg = avg / dble( nSize )
60 std = std / dble( nSize )
61 std = sqrt( std - avg**2 )
62 write(6,*) 'avg :: ', avg, 'std :: ', std
63
64 return
65end program main
gaussElimMod.f90¶
1! ====================================================== !
2! === gauss Elimination :: partial pivoting ver. === !
3! ====================================================== !
4module gaussElimMod
5contains
6
7 ! ========================================================== !
8 ! === Gauss Elimination Solver === !
9 ! ========================================================== !
10 subroutine gaussElimin( Amat, xvec, bvec, nSize )
11 implicit none
12 integer , intent(in) :: nSize
13 double precision, intent(in) :: Amat(nSize,nSize)
14 double precision, intent(in) :: bvec(nSize)
15 double precision, intent(out) :: xvec(nSize)
16 integer :: i, j, k, ipivot
17 double precision :: Dinv, buff, vpivot
18 double precision, parameter :: eps = 1.d-10
19 double precision, allocatable :: Umat(:,:), vvec(:,:)
20
21 ! ----------------------------------------- !
22 ! --- [1] Preparation --- !
23 ! ----------------------------------------- !
24 ! -- [1-1] allocate Umat -- !
25 allocate( Umat(nSize,nSize) )
26 ! -- [1-2] Copy AMat & bvec -- !
27 Umat(:,:) = Amat(:,:)
28 xvec(:) = bvec(:)
29
30 ! ----------------------------------------- !
31 ! --- [2] Forward Ellimination --- !
32 ! ----------------------------------------- !
33 do k=1, nSize
34
35 ! -- [2-1] Pivoting -- !
36 vpivot = abs( Umat(k,k) )
37 ipivot = k
38 do j=k+1, nSize
39 if ( abs( Umat(j,k) ).gt.vpivot ) then
40 vpivot = abs( Umat(j,k) )
41 ipivot = j
42 endif
43 end do
44 if ( ipivot.ne.k ) then
45 do j=k, nSize
46 buff = Umat(ipivot,j)
47 Umat(ipivot,j) = Umat(k ,j)
48 Umat(k ,j) = buff
49 enddo
50 buff = xvec(ipivot)
51 xvec(ipivot) = xvec(k)
52 xvec(k) = buff
53 end if
54 if ( abs( Umat(k,k) ).lt.eps ) then
55 write(6,*) '[gaussElimin] Amat :: Singular Matrix :: No Solution End :: @ k= ', k
56 stop
57 endif
58 ! -- [2-2] Diagonal Component -- !
59 Dinv = 1.d0 / Umat(k,k)
60 Umat(k,k) = 1.d0
61
62 ! -- [2-3] Non-Diagonal Component -- !
63 if ( k.eq.nSize ) then
64 ! -- [ Last Row :: k == nSize ] -- !
65 xvec(k) = Dinv * xvec(k)
66 else
67 ! -- [Not Last Row :: k != nSize ] -- !
68 ! - Division - !
69 Umat(k,k+1:nSize) = Dinv * Umat(k,k+1:nSize)
70 xvec(k) = Dinv * xvec(k)
71 ! - subtraction - !
72 do j=k+1,nSize
73 Umat(j,k+1:nSize) = Umat(j,k+1:nSize) - Umat(j,k) * Umat(k,k+1:nSize)
74 xvec(j) = xvec(j) - Umat(j,k) * xvec(k)
75 Umat(j,k) = 0.d0
76 enddo
77 endif
78
79 end do
80
81 ! ----------------------------------------- !
82 ! --- [3] Backward Substituition --- !
83 ! ----------------------------------------- !
84 do k=nSize-1, 1, -1
85 do i=nSize, k+1, -1
86 xvec(k) = xvec(k) - Umat(k,i)*xvec(i)
87 enddo
88 enddo
89
90 return
91 end subroutine gaussElimin
92
93end module gaussElimMod
Gauss の消去法のサンプル実行結果¶
実行結果を以下に示す．1段目に与えた行列 A と左辺ベクトル b を示している．2段目には、得た解 x 、及び、解の正しさを示すために、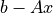 
とその誤差を計算している．
