LU分解¶
LU分解 ( LU-Decomposition ) は任意の正則行列に対して成り立つ、行列分解手法である． 行列 A が正則であるならば、
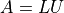
と、下三角行列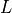 
と上三角行列 
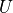積に分解することができる．これを LU分解 と呼ぶ．
LU分解は、 Gauss の消去法における前進消去による上三角行列化に他ならない．行列 A と単位行列 E の拡大係数行列に対して、前進消去を適用し、上三角行列化する．
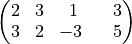
ここで、前進消去に要した行基本変形をまとめて 行列 K と表現すれば、
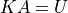
である．ここで、行列 K は下三角行列であり、この逆行列も下三角行列となる．両辺に K の逆行列 ( L とおく )を左からかけることにより、
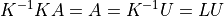
と書くことができる．行列 L は下三角行列であり、行列 U は上三角行列であることから、一連の操作はAに対するLU分解である．つまり、Gaussの消去法における前進消去はLU分解に他ならないことがわかる．
LU分解のサンプルコード¶
LU分解のサンプルコードについて、以下に示す．
main.f90¶
1! ====================================================== !
2! === Gauss Jordan Inverting Example === !
3! ====================================================== !
4program main
5 use LU_DecompMod, only : LU_Decomposition, LU_BackSubstitution, LU_MatrixInverse
6 implicit none
7 character(100) , parameter :: AmatFile = 'dat/Amat.dat'
8 character(100) , parameter :: LmatFile = 'dat/Lmat.dat'
9 character(100) , parameter :: UmatFile = 'dat/Umat.dat'
10 character(100) , parameter :: bvecFile = 'dat/bvec.dat'
11 double precision, allocatable :: Amat(:,:), Lmat(:,:), Umat(:,:)
12 double precision, allocatable :: Bmat(:,:), Ainv(:,:)
13 double precision, allocatable :: bvec(:), xvec(:), avec(:)
14 integer , allocatable :: indx(:)
15 integer :: i, j, nSize, nSize_
16 integer , parameter :: lun = 50
17
18 ! ------------------------------------- !
19 ! --- [1] Data Load --- !
20 ! ------------------------------------- !
21 open(lun,file=trim(AmatFile),status='old',form='formatted')
22 read(lun,*) nSize, nSize
23 allocate( Amat(nSize,nSize), Lmat(nSize,nSize), Umat(nSize,nSize) )
24 allocate( Bmat(nSize,nSize), Ainv(nSize,nSize) )
25 allocate( indx(nSize) )
26 Amat(:,:) = 0.d0
27 Lmat(:,:) = 0.d0
28 Umat(:,:) = 0.d0
29 Bmat(:,:) = 0.d0
30 do i=1, nSize
31 read(lun,*) Amat(i,:)
32 enddo
33 close(lun)
34 open(lun,file=trim(bvecFile),status='old',form='formatted')
35 read(lun,*) nSize_
36 if ( nSize.ne.nSize_ ) stop '[main] incompatible size Amat vs. bvec ERROR !!!'
37 allocate( bvec(nSize), xvec(nSize), avec(nSize) )
38 do i=1, nSize
39 read(lun,*) bvec(i)
40 enddo
41 close(lun)
42
43 ! ------------------------------------- !
44 ! --- [2] LU Decomposition & solve --- !
45 ! ------------------------------------- !
46 call LU_Decomposition ( Amat, Lmat, Umat, indx, nSize )
47 call LU_BackSubstitution( Lmat, Umat, bvec, xvec, indx, nSize )
48 call LU_MatrixInverse ( Amat, Ainv, nSize )
49
50 ! ------------------------------------- !
51 ! --- [3] save Results --- !
52 ! ------------------------------------- !
53 open(lun,file=trim(LmatFile),status='replace',form='formatted')
54 write(lun,*) nSize
55 do i=1, nSize
56 write(lun,*) Lmat(i,:)
57 enddo
58 open(lun,file=trim(UmatFile),status='replace',form='formatted')
59 write(lun,*) nSize
60 do i=1, nSize
61 write(lun,*) Umat(i,:)
62 enddo
63 close(lun)
64 ! ------------------------------------- !
65 ! --- [4] confirm results --- !
66 ! ------------------------------------- !
67 ! -- [4-1] input Amatrix -- !
68 write(6,*)
69 write(6,*) 'Amat (input) '
70 do i=1, nSize
71 write(6,*) Amat(i,:)
72 enddo
73 ! -- [4-2] LU Decomposition -- !
74 write(6,*)
75 write(6,*) 'Lmat | Umat (decomposed results) '
76 do i=1, nSize
77 write(6,*) Lmat(i,:), ' | ', Umat(i,:)
78 enddo
79 write(6,*)
80 write(6,*) 'LU ( multiplied matrix )'
81 Bmat = matmul( Lmat, Umat )
82 do i=1, nSize
83 write(6,*) Bmat(i,:)
84 enddo
85 write(6,*)
86 write(6,*) 'A* ( permutated A matrix ) must be LU'
87 do i=1, nSize
88 write(6,*) Amat(indx(i),:)
89 enddo
90 write(6,*)
91 write(6,*) 'permutation index ( i-th row ==> indx(i) )'
92 do i=1, nSize
93 write(6,*) i, indx(i)
94 enddo
95 ! -- [4-3] solve eqs. -- !
96 write(6,*)
97 write(6,*) 'b ( L.H.S. )'
98 do i=1, nSize
99 write(6,*) bvec(i)
100 enddo
101 write(6,*)
102 write(6,*) 'x ( Numerical Solution )'
103 do i=1, nSize
104 write(6,*) xvec(i)
105 enddo
106 avec(:) = matmul( Amat, xvec )
107 write(6,*)
108 write(6,*) 'residual of the solution ( for A-Matrix )'
109 do i=1, nSize
110 write(6,*) avec(i)
111 enddo
112 avec(:) = matmul( Bmat, xvec )
113 write(6,*)
114 write(6,*) 'residual of the solution ( for LU-matrix )'
115 do i=1, nSize
116 write(6,*) avec(i)
117 enddo
118 ! -- [4-4] inverted Amat :: Ainv -- !
119 write(6,*) 'A^-1 ( inverted A matrix )'
120 do i=1, nSize
121 write(6,*) Ainv(i,:)
122 enddo
123 write(6,*)
124 write(6,*) 'A^-1 A must be unit matrix'
125 Bmat(:,:) = matmul( Ainv, Amat )
126 do i=1, nSize
127 write(6,*) Bmat(i,:)
128 enddo
129 write(6,*)
130 write(6,*) 'A A^-1 must be unit matrix'
131 Bmat(:,:) = matmul( Amat, Ainv )
132 do i=1, nSize
133 write(6,*) Bmat(i,:)
134 enddo
135 write(6,*)
136
137 return
138end program main
LU_DecompMod.f90¶
1module LU_DecompMod
2contains
3
4 ! ====================================================== !
5 ! === LU Decomposition Routines === !
6 ! ====================================================== !
7 subroutine LU_Decomposition( Amat, Lmat, Umat, indx, nSize )
8 implicit none
9 integer , intent(in) :: nSize
10 double precision, intent(in) :: Amat(nSize,nSize)
11 double precision, intent(out) :: Lmat(nSize,nSize), Umat(nSize,nSize)
12 integer , intent(out) :: indx(nSize)
13 integer :: i, j, k, iMax, ibuff
14 double precision, allocatable :: Bmat(:,:), vv(:)
15 double precision :: BBMax, dbuff, sum
16 double precision, parameter :: eps = 1.d-20
17 ! ------------------------------------------------------ !
18 ! -- indx(nSize) :: permutation index. -- !
19 ! -- to avoid Numerical error -- !
20 ! -- ( == pivot selection) -- !
21 ! -- LU(i,:) = A( indx(i),: ) -- !
22 ! ------------------------------------------------------ !
23
24 ! ------------------------------------------------------ !
25 ! --- [1] Singular Matrix Detection & vv Info --- !
26 ! ------------------------------------------------------ !
27 ! -- [1-1] prepare index / Bmat -- !
28 allocate( Bmat(nSize,nSize), vv(nSize) )
29 do i=1, nSize
30 indx(i) = i
31 enddo
32 do j=1, nSize
33 do i=1, nSize
34 Bmat(i,j) = Amat(i,j)
35 enddo
36 enddo
37 ! -- [1-2] large value check for permutation -- !
38 do i=1, nSize
39 BBMax = 0.d0
40 do j=1, nSize
41 if ( abs( Bmat(i,j) ).gt.BBMax ) BBMax = abs( Bmat(i,j) )
42 enddo
43 if ( BBmax.eq.0.d0 ) then
44 write(6,*) "[LU_Decomposition] Singular Matrix !!! ERROR !!!"
45 endif
46 vv(i) = 1.d0 / BBMax
47 enddo
48 ! ------------------------------------------------------ !
49 ! --- [2] Main Loop of the LU Decomposition --- !
50 ! ------------------------------------------------------ !
51 do j=1, nSize ! -- main loop -- !
52 ! -- [2-1] col-wise ( horizontal scan ) -- !
53 do i=1, j-1
54 sum = Bmat(i,j)
55 do k=1, i-1
56 sum = sum - Bmat(i,k)*Bmat(k,j)
57 enddo
58 Bmat(i,j) = sum
59 enddo
60 BBMax = 0.d0
61 ! -- [2-2] row-wise ( vertical scan ) -- !
62 do i=j, nSize
63 sum = Bmat(i,j)
64 do k=1, j-1
65 sum = sum - Bmat(i,k)*Bmat(k,j)
66 enddo
67 Bmat(i,j) = sum
68 dbuff = vv(i) * abs(sum)
69 if ( dbuff.ge.BBMax ) then
70 iMax = i
71 BBMax = dbuff
72 endif
73 enddo
74 ! -- [2-3] permutation :: exchange Bmat & indx -- !
75 if ( j.ne.iMax ) then
76 do k=1, nSize
77 dbuff = Bmat(iMax,k)
78 Bmat(iMax,k) = Bmat(j,k)
79 Bmat(j,k) = dbuff
80 enddo
81 vv(iMax) = vv(j)
82 ibuff = indx(j)
83 indx(j) = indx(iMax)
84 indx(iMax) = ibuff
85 endif
86 ! -- [2-4] singular matrix :: mild prescription -- !
87 if ( Bmat(j,j).eq.0.d0 ) then
88 Bmat(j,j) = eps
89 endif
90 ! -- [2-5] Diagonal component 1 / D -- !
91 if ( j.ne.nSize ) then
92 dbuff = 1.d0 / Bmat(j,j)
93 do i=j+1, nSize
94 Bmat(i,j) = Bmat(i,j) * dbuff
95 enddo
96 endif
97 enddo ! -- main loop end -- !
98 ! ------------------------------------------------------ !
99 ! --- [3] store Lmat & Umat for easy use --- !
100 ! ------------------------------------------------------ !
101 do i=1, nSize
102 ! -- [3-1] B( i, j=1~i-1 ) ==> Lmat -- !
103 do j=1, i-1
104 Lmat(i,j) = Bmat(i,j)
105 enddo
106 ! -- [3-2] Diagonal Component of Lmat == 1 -- !
107 Lmat(i,i) = 1.d0
108 ! -- [3-3] B( i, j=i~nSize ) ==> Umat -- !
109 do j=i, nSize
110 Umat(i,j) = Bmat(i,j)
111 enddo
112 enddo
113 return
114 end subroutine LU_Decomposition
115
116
117 ! ====================================================== !
118 ! === Backward Substitution Method === !
119 ! ====================================================== !
120 subroutine LU_BackSubstitution( Lmat, Umat, bvec, xvec, indx, nSize )
121 implicit none
122 integer , intent(in) :: nSize
123 integer , intent(in) :: indx(nSize)
124 double precision, intent(in) :: bvec(nSize)
125 double precision, intent(in) :: Lmat(nSize,nSize), Umat(nSize,nSize)
126 double precision, intent(out) :: xvec(nSize)
127 integer :: i, j, ii, ll
128 double precision :: sum
129
130 ! ------------------------------------------------------ !
131 ! --- [1] prepare for back substition --- !
132 ! ------------------------------------------------------ !
133 do i=1, nSize
134 xvec(i) = bvec(indx(i))
135 enddo
136 ! ------------------------------------------------------ !
137 ! --- [2] solve Ly = b ( Ax = LUx = Ly = b ) --- !
138 ! ------------------------------------------------------ !
139 ii=0
140 do i=1, nSize
141 sum = xvec(i)
142 if ( ii.ne.0 ) then
143 do j=ii,i-1
144 sum = sum - Lmat(i,j) * xvec(j)
145 enddo
146 else if ( sum.ne.0 ) then
147 ii = i
148 endif
149 xvec(i) = sum
150 enddo
151 ! ------------------------------------------------------ !
152 ! --- [3] solve Ux = y using above y --- !
153 ! ------------------------------------------------------ !
154 do i=nSize, 1, -1
155 sum = xvec(i)
156 do j=i+1, nSize
157 sum = sum - Umat(i,j) * xvec(j)
158 end do
159 xvec(i) = sum / Umat(i,i)
160 enddo
161
162 return
163 end subroutine LU_BackSubstitution
164
165
166 ! ====================================================== !
167 ! === LU_MatrixInverse === !
168 ! ====================================================== !
169 subroutine LU_MatrixInverse( Amat, Ainv, nSize )
170 implicit none
171 integer , intent(in) :: nSize
172 double precision, intent(in) :: Amat(nSize,nSize)
173 double precision, intent(out) :: Ainv(nSize,nSize)
174 integer :: i, j
175 integer , allocatable :: indx(:)
176 double precision, allocatable :: Lmat(:,:), Umat(:,:), xvec(:), bvec(:)
177
178 ! ------------------------------------------------------ !
179 ! --- [1] preparation of matrix & indx --- !
180 ! ------------------------------------------------------ !
181 allocate( Lmat(nSize,nSize), Umat(nSize,nSize), indx(nSize) )
182 allocate( xvec(nSize), bvec(nSize) )
183 do j=1, nSize
184 do i=1, nSize
185 Ainv(i,j) = 0.d0
186 enddo
187 Ainv(j,j) = 1.d0
188 enddo
189 ! ------------------------------------------------------ !
190 ! --- [2] LU Decomposition --- !
191 ! ------------------------------------------------------ !
192 call LU_Decomposition( Amat, Lmat, Umat, indx, nSize )
193 ! ------------------------------------------------------ !
194 ! --- [3] matrix Inversion by back-substitution --- !
195 ! ------------------------------------------------------ !
196 do j=1, nSize
197 do i=1, nSize
198 xvec(i) = 0.d0
199 bvec(i) = Ainv(i,j)
200 enddo
201 call LU_BackSubstitution( Lmat, Umat, bvec, xvec, indx, nSize )
202 do i=1, nSize
203 Ainv(i,j) = xvec(i)
204 enddo
205 enddo
206
207 return
208 end subroutine LU_MatrixInverse
209
210
211end module LU_DecompMod
LU分解のサンプル実行結果¶
実行結果を以下に示す．まずは、LU分解単体でのテストケースについて．
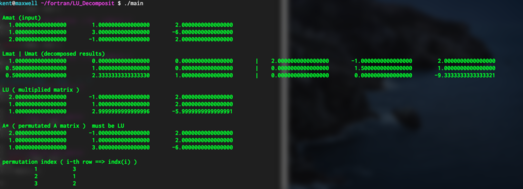
1段目に入力した行列Aを表示し、2段目に行列AのLU分解結果を示している．3段目には、LU分解の確認のために、行列積LUを計算している．ここで、LU分解の際には部分ピボット選択のために行の入れ替わりが生じている．そこで、行の入れ替えを考慮した行列Aを4段目に表示しており、これがLU積と一致していることから正しくLU分解できていることがわかる．最後には、ピボット選択による入れ替え結果( indx )を示している．
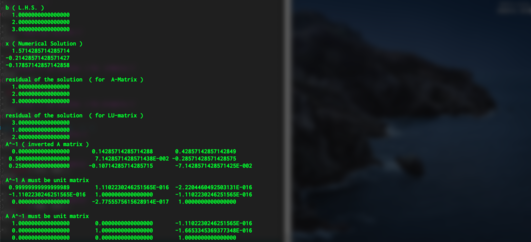
次に、LU分解を用いた連立方程式の求解について検証している．上記、行列 A に対して与える左辺ベクトル b を1段目に示している．これを解くと次段に示した解が得られた．Ax、 及び、LUxを計算してやると3,4段目となり、入力した 左辺ベクトル b と一致していることがわかる．
次に、行列 A の逆行列をLU分解によって求めた結果を5段目に示す．これは、 Gauss-Jordan 法で解いた結果と一致しており、また、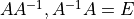 
を6,7段目に示した．
