重み付け残渣法の種類

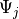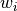試行関数 \Psi_j ，重み関数 w_i を決定して，体積積分を実行すると，積分部分は係数行列となり，線形連立方程式の解として係数列 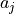a_j は表された．逆行列を求めて係数列を求めれば，試行関数の重ね合わせによって近似解が構成できる．ここで，疑問となるのは，重み関数 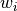w_i はどのようなものを用いれば良いか，である．以下に重み関数をどのようなものを用いれば良いかを例に挙げる．結論を先に述べると，『いつ，いかなる時も， Galerkin 法を使えば大体間違いない』である．

選点法 (collocation Method)

重み関数として，デルタ関数 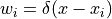w_i=\delta( x -x_i ) を使う．

デルタ関数 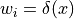w_i=\delta( x ) の性質から，

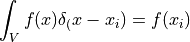
\int_V f(x) \delta_(x-x_i) = f(x_i)

であるから，

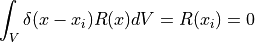
\int_V \delta( x - x_i ) R(x) dV = R(x_i) = 0

選点法(collocation Method)は，領域内の任意のn個の点 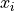x_i を選び出して，それぞれの位置でピッタリ合わせる( 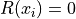R(x_i)=0 )ようにして，ペタペタとフィッティングをかけるのである．要は，『n点選んでそこだけはピッタリ合わせましょうね』法である．

最小二乗法 (Least Squared Method)

重み関数として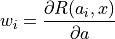， w_i=\dfrac{ \partial R(a_i,x) }{ \partial a } を使う． 何故，この重み関数が最小二乗解を与えるのであろうか？以下に示す． 最小二乗法は代表的な最適化手法である．誤差二乗値は

I[R(a_j,x)] = \int_V [ R(a_j,x) ]^2 dV

であり，これを極小値で停留させることを考える．条件式は

\dfrac{\partial }{\partial a_j}[ I(a_j) ] = \int_V 2 R(a_j,x) \dfrac{\partial R(a_j,x) }{\partial a_j} = 0 \ \ \ \ (j=1,2,\cdots,N)

と書ける．これと重み付け残差法の式，

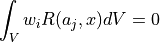
\int_V w_i R(a_j,x) dV = 0

を見比べれば，すぐさま 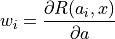w_i=\dfrac{ \partial R(a_i,x) }{ \partial a } が最小二乗法と同等の解を与えることがわかる．

Galerkin 法( Glearkin Method )

重み関数として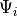， \Psi_i を用いる．

Galerkin 法は有限要素法で広く使用されている手法である．ほとんどの場合で， Galerkin 法が精度の良い解を与えるらしい．何故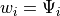， w_i=\Psi_i (重み関数を試行関数)とすればうまくいくのか？ これは変分法 ( Ritz 法 )と関係しているらしい．ここでは概要だけ述べることに留める．「重み関数をどういった関数にすれば良いか？」という問いに対しては，重み関数を汎関数として考えれば，誤差を最小にする汎関数は何かという変分問題に書ける．このようにして，最も誤差の少ない重み関数を求める手法を Ritz 法という．有限要素法における定式化において，次が成り立つ．

Note

重み付け残差法において，誤差を最小にする重み関数を考える．もし，そのような重み関数に汎関数が存在するとき， Ritz 法による重み関数及び解と Galerkin 法による重み関数及び解は，それぞれ一致する．

このことから， Galerkin 法は汎関数が存在する問題において， Rits 法（変分原理）によって，最も良い重み関数を採用しているということが保証されるのである．一方で， Galerkin 法では，実際に変分法を駆使して重み関数を導出したりすることがなく，定めた試行関数を 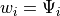w_i=\Psi_i として用いるだけであり，簡便である．このことから， Galearkin 法は精度良く簡便な手法として有限要素法で広く用いられている．