1次元熱拡散方程式の定常解に対する有限要素解析(定式化編)¶
厳密解¶
x=0でT=0の熱浴に接触した熱伝導係数 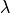 ,熱生成項
,熱生成項 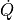 の断面積
の断面積 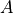 の棒状の物質を考える.系は1次元の並進対称系とする.支配方程式は,
の棒状の物質を考える.系は1次元の並進対称系とする.支配方程式は,
![\dfrac{ \partial }{ \partial x } [ \lambda \dfrac{ \partial T }{ \partial x } ] + \dot{Q} = 0](../../_images/math/7b847678dcf32056fbc8b3532695104e299f504a.png)
この解のうち,熱伝導係数も熱生成項も位置によらず,一定であった場合を考える.
両辺積分して,
![\lambda \dfrac{ \partial T }{ \partial x } = - \int \dot{Q} dx = - \dot{Q} [ x + C_1 ]](../../_images/math/a926c36eda5f075b40958f642e040456f1a88b03.png)
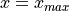 における自由境界条件
における自由境界条件 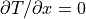 より,
より,
![\partial T / \partial x (x=x_{max}) &= - \dfrac{\dot{Q}}{\lambda} [x+C_1] = 0 \\
C_1 &= - x_{max}](../../_images/math/9f55ffb10dac8e500f7b0dfc5315f829be081555.png)
再度積分して
![T = - \dfrac{ \dot{Q} }{ \lambda } [ \dfrac{1}{2} x^2 - x_{max} x + C_2 ]](../../_images/math/952c049852c5d56b7a1983904ce232f4216db6b1.png)
固定端境界条件 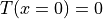 を用いて,
を用いて,
![T &= - \dfrac{ \dot{Q} }{ \lambda } [ C_2 ] = 0 \\
C_2 &= 0](../../_images/math/69e214e92dbf926471e78193f77a883da1ebf318.png)
上記より,
![T = - \dfrac{ \dot{Q} }{ \lambda } [ x ( \dfrac{1}{2} x - x_{max} ) ]](../../_images/math/144dbc1e8ae4d3b412ab43e0588c3ae8b79a537c.png)
が解となる.
近似解を代入して考えてみる¶
区間 ![[X_k,X_{k+1}]](../../_images/math/c715c3a1aa8af5c5a67b49a602f62215b8ed81f0.png) に存在する
に存在する 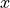 における温度を各接点の情報
における温度を各接点の情報 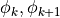 から例えば 1次要素 (線形近似) を用いて表す.
から例えば 1次要素 (線形近似) を用いて表す.
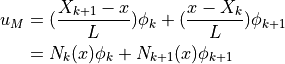
ここで, 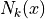 は点kに関する形状関数で位置xの関数である. 上式では線形要素を例として表記したが,1次以上の形状関数を用いても同様に表すことができ,位置
は点kに関する形状関数で位置xの関数である. 上式では線形要素を例として表記したが,1次以上の形状関数を用いても同様に表すことができ,位置 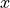 における解
における解 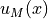 は一般に次のように表せる.
は一般に次のように表せる.
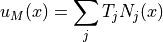
これは,試行関数の重ね合わせによる近似解( 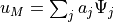 )に他ならない.
)に他ならない.
区間 ![[X_k,X_{k+1}]](../../_images/math/c715c3a1aa8af5c5a67b49a602f62215b8ed81f0.png) の間の解は上式のように形状関数の重ね合わせで表すことができる.
重ね合わせは次のようにベクトルによる内積の表式を用いればスッキリと表せる.
の間の解は上式のように形状関数の重ね合わせで表すことができる.
重ね合わせは次のようにベクトルによる内積の表式を用いればスッキリと表せる.
![u_M(x) = [N] \{ \phi \}](../../_images/math/6cd108bfd16dc4065717614b0eafadd61dd69e67.png)
ここで, 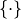 は 縦ベクトル ,
は 縦ベクトル , ![[\cdot]](../../_images/math/86b755835f705e35d51b6e308b16c6f5e97438af.png) は 横ベクトル を表している.
上記の連立方程式は問題を分割したひとつの要素に注目して得られていることを強調しておく.
つまり,問題全体として,方程式は [要素分割数]個 できることになる.
は 横ベクトル を表している.
上記の連立方程式は問題を分割したひとつの要素に注目して得られていることを強調しておく.
つまり,問題全体として,方程式は [要素分割数]個 できることになる.
Green の定理の適用¶
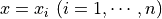 における任意の重み関数
における任意の重み関数 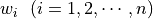 を考え,重み付き残差法の式
を考え,重み付き残差法の式 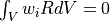 に対して 1次元の Green の定理
に対して 1次元の Green の定理 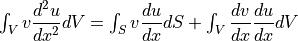 を適用する.
を適用する.
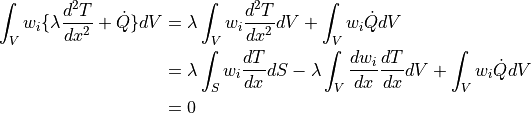
ここに,要素分割による形状関数による近似 ![T=u_M = [N] \{\phi\}{}](../../_images/math/36c654922676aa9e99d18ff641cebff91ec9cc58.png) を代入すれば,
を代入すれば,
![\lambda \int_V \dfrac{d w_i }{dx} \dfrac{d [N]}{dx} \{\phi\} dV = \lambda \int_S w_i \dfrac{d [N]}{dx} \{\phi\} dS + \int_V w_i \dot{Q} dV](../../_images/math/a5fcbd6ea9575e3d117c8678c62cf62eb10773a2.png)
となる.面積分項は流束を用いて,
![\lambda \int_S w_i \dfrac{d [N]}{dx} \{\phi\} dS = - \int_S w_i q dS](../../_images/math/29513e1c5dba7e4ee799bbb8dfe997314643fa1e.png)
と表すことができ,隣接する要素間で流出量と流入量は打ち消しあい,要素内部では意味を持たない. この項は境界条件においてのみ意味をもつ.このように表すと,
![\lambda \int_V \dfrac{d w_i }{dx} \dfrac{d [N]}{dx} \{\phi\} dV = - \int_S w_i q dS + \int_V w_i \dot{Q} dV](../../_images/math/b2e3fab5244cdd6e185fbf4f5e35571681e2bfdf.png)
ここでは, 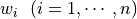 に対する式を導出した.重み関数はn個の節点情報を求めるために,n個用いることで方程式系を閉じさせる.これらをベクトルによってまとめて取り扱うように次のように表記しておく.
に対する式を導出した.重み関数はn個の節点情報を求めるために,n個用いることで方程式系を閉じさせる.これらをベクトルによってまとめて取り扱うように次のように表記しておく.
![\lambda \int_V \dfrac{d \{w\} }{dx} \dfrac{d [N]}{dx} \{\phi\} dV = - \int_S \{w\} q dS + \int_V \{w\} \dot{Q} dV](../../_images/math/eb8ab3650dc9d474e90a0dc815c0b755a4110d6c.png)
Galerkin 法の適用¶
Galerkin 法では, 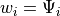 を採用する.ここでは,
を採用する.ここでは, ![\{w\}=[N]^{T}](../../_images/math/09f743b343736578e6c18249b36280d79021ea66.png) とすれば良い.
とすれば良い.
![\lambda \int_V \dfrac{d [N]^{T} }{dx} \dfrac{d [N]}{dx} \{\phi\} dV = - \int_S [N]^T q dS + \int_V [N]^T \dot{Q} dV](../../_images/math/2a47f43ae8ca42dc83d976c0ac080dc50027822f.png)
上式が Galerkin法における有限要素法の式 である. 今,節点変数を除いた部分を
![[k] ^{e} &= \lambda \int_V \dfrac{d [N]^{T} }{dx} \dfrac{d [N]}{dx} dV \\
\{f\}^{e} &= - \int_S [N]^T q dS + \int_V [N]^T \dot{Q} dV](../../_images/math/c648d6211d31069583b8fdfa8f85ab484e547205.png)
とおけば,各有限要素における近似解は,
![[k]^{(e)} \{ \phi \}^{(e)} = \{ f \}^{(e)}](../../_images/math/cdf08fd53e355ce5d15a6ef6ff21fab9024d6223.png)
と書ける.
ここで,上付き(e)は要素毎( by element )の式であることを意味しており,分割した要素を全て集めると,解くべき式の行列表現となる.
行列表現の意味するところは,勿論,有限要素法の帰着する先が連立方程式であることである.
つまり,行列反転さえ行えば,節点変数である 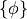 が求解可能である.
が求解可能である.
![[k]^{(e)}](../../_images/math/44942303d534c1492f6059fafe93d490cf8eed84.png) 及び
及び 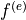 の計算¶
の計算¶
左辺のk-Matrix(k-マトリクス),及び,右辺のf-vector(f-ベクトル)を求めれば,ある要素における節点情報を解くことができる.
これらを規定しているのは,形状関数 ![[N]](../../_images/math/6a04c93c809b8bd990a73630a9ec01a92db9c13e.png) であるので,例として再度1次要素を取り上げて,計算を行う.
であるので,例として再度1次要素を取り上げて,計算を行う.
区間 ![[X_k,X_{k+1}]](../../_images/math/c715c3a1aa8af5c5a67b49a602f62215b8ed81f0.png) の端部2節点による形状関数は
の端部2節点による形状関数は
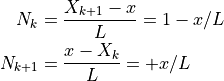
であるから,これらの微分は以下になる.
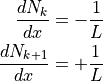
ベクトルとしてまとめて表記すると,
![[N] =
\begin{bmatrix}
\dfrac{X_{k+1}-x}{L} & \dfrac{x-X_{k }}{L}
\end{bmatrix}](../../_images/math/bbbb2683e5a52a82f028a4b5157a7a069f29f7f7.png)
![\dfrac{ d [N] }{ dx } =
\begin{bmatrix}
- \dfrac{1}{L} & + \dfrac{1}{L}
\end{bmatrix}](../../_images/math/12aceb5dd3314f9c79001ab343e6b2f6240d8fcd.png)
である.これを用いて,要素毎のk-Matrixを求めると,
![[k]^{e}
&= \int_V \lambda ( \dfrac{d[N]^T}{dx} \dfrac{d[N]}{dx} ) dV \\
&= \lambda \int_0^L
\begin{bmatrix}
- \dfrac{1}{L} \\
+ \dfrac{1}{L}
\end{bmatrix}
\begin{bmatrix}
- \dfrac{1}{L} & + \dfrac{1}{L}
\end{bmatrix}
A
dx \\
&= \dfrac{ \lambda A }{ L^2 } \int_0^L
\begin{bmatrix}
+1 & -1 \\
-1 & +1
\end{bmatrix}
dx \\
&= \dfrac{ \lambda A }{ L }
\begin{bmatrix}
+1 & -1 \\
-1 & +1
\end{bmatrix}](../../_images/math/7f819fd3688d981e54f3e06e5ac2ca65d990c603.png)
次に,f-vectorを項別に求めると,
(熱生成項)
![\int_V [N]^T \dot{Q} dV
&= \int_{0}^{L}
\begin{bmatrix}
1-x/L \\
+x/L
\end{bmatrix}
\dot{Q} A dx \\
&= \dot{Q} A
[
\begin{bmatrix}
x - \dfrac{x^2}{2L} \\
+ \dfrac{x^2}{2L}
\end{bmatrix}
]_0^L
= \dot{Q} A
\begin{bmatrix}
+ \dfrac{1}{2}L \\
+ \dfrac{1}{2}L
\end{bmatrix} \\
&= \dfrac{ \dot{Q} AL }{2}
\begin{bmatrix}
1 \\
1
\end{bmatrix}](../../_images/math/bc727de0af06411fed00ce687445562453f2447f.png)
(熱流束項)
![\int_S [N]^T q dS
= q A \|_{x=L}
= q A
\begin{bmatrix}
0 \\
1
\end{bmatrix}](../../_images/math/3e1c5a85d40d691f4acca6c7dd3add38e9f02260.png)
ここで,熱流束項は自由境界端部でのみ作用する.
以上の導出から,とある要素における有限要素法が満たすべき連立方程式は,
![[k]^{(e)} \{ \phi \}^{(e)} &= \{ f \}^{(e)} \\
\dfrac{ \lambda A }{ L }
\begin{bmatrix}
+1 & -1 \\
-1 & +1
\end{bmatrix}
\begin{bmatrix}
\phi_{k} \\
\phi_{k+1}
\end{bmatrix}
&= \dfrac{ \dot{Q} AL }{2}
\begin{bmatrix}
1 \\
1
\end{bmatrix}
- q A
\begin{bmatrix}
0 \\
1
\end{bmatrix} _{if \ ( k \ is \ edge )}](../../_images/math/318551ebac87bdbbebcf3a996abb4b8af4e89972.png)
この連立方程式を解いて, ![[\phi_k,\phi_{k+1}]](../../_images/math/e200184c8c67e1252132b63241c7fe213aad0322.png) を求めれば,節点温度を解析得ることができる.
これは要素一つだけに着目した解であり,境界条件が影響しない要素はほぼ無意味な端部条件による解しか得られない.
実際には,境界条件から情報が内部のセルへ浸透していき,端部での節点温度の求解が内部領域の節点温度として作用していくので,要素全体で一斉に解を得ることが正しい解を得るために必須となる.
を求めれば,節点温度を解析得ることができる.
これは要素一つだけに着目した解であり,境界条件が影響しない要素はほぼ無意味な端部条件による解しか得られない.
実際には,境界条件から情報が内部のセルへ浸透していき,端部での節点温度の求解が内部領域の節点温度として作用していくので,要素全体で一斉に解を得ることが正しい解を得るために必須となる.
つまり,これまでに導出した要素方程式系( Element Matrix & Element Equations )を集めて,系全体の方程式系 ( Global Matrix & Global Equations )を構成する必要がある.これは決して難しいことではなく,単に集合させるだけで良い.結果,要素行列をまとめたGlobal Matrixが以下のように定義される.
![[K] &= \sum [k] \\
\{ \Phi \} &= \sum \{ \phi \} \\
\{ F \} &= \sum \{ f \}](../../_images/math/a66b59fe4cc35e0cc86f2250d3c98d66c3bcc71f.png)
解くべき Global Equationsを,次式に表す.
![[K] \{ \Phi \} = \{ F \}](../../_images/math/40c2b2e61630f933b42939d9a7926ccf7d416165.png)
Global Equationsを行列反転させれば,有限要素法によって得たい解 (ここでは1次元熱拡散方程式の定常解)を得ることができる.
