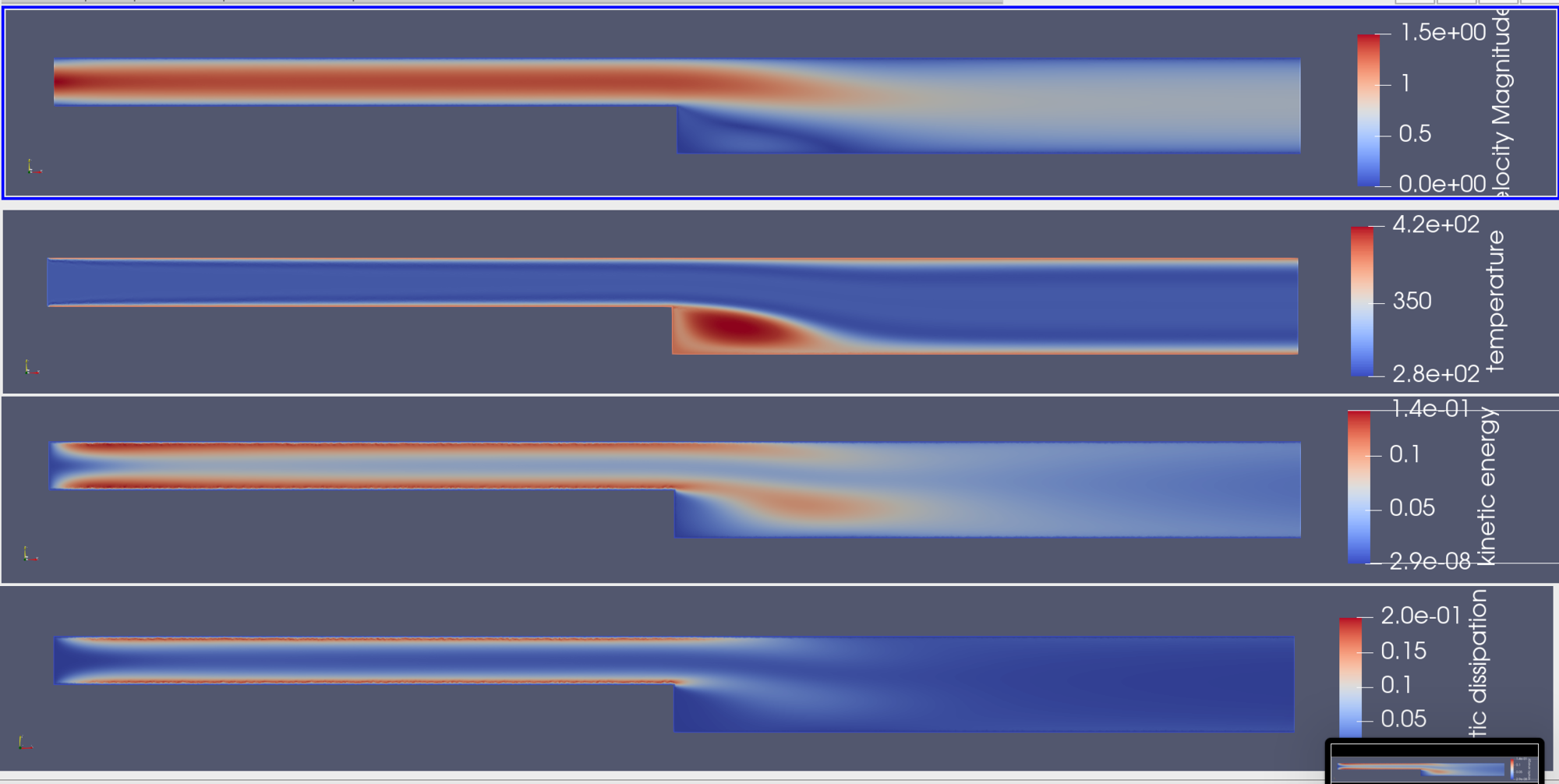
バックステップ流れでの壁面からの熱輸送¶
シミュレーション名 :: thermalFluid__backStep_XY2D
シミュレーション体系¶
基本方程式は、 Navier-Stokes方程式 と 標準k-ε方程式 と 熱輸送方程式
流体は、 非圧縮 , 標準k-εモデル を取扱い、対象は空気とする.
計算対象は、いわゆるバックステップ流れと呼ばれるものである.
2次元 長さ 13 [m], 幅 1 [m] の流路から、長さ 13 [m] 、幅 2 [m] の流路への切り替わる.
流入境界は、ポワズイユ流れとし、流出境界は uy=0 とする.
標準k-εモデル を用いて、壁境界は 滑りなし壁条件を課した.
全領域の初期条件は、流速は0、k=0.00457, epsilon=1e-4 とおいている.
別計算( flow__backStep_keSolver_XY2D ) に熱輸送方程式をカップルしている
物性条件¶
Target |
Parameters |
Value |
Unit |
Description |
|---|---|---|---|---|
空気 |
Density |
1.2e+0 |
kg/m3 |
密度 |
viscosity |
1.0e-5 |
Pa.s |
粘度 |
|
KE SigmaK |
1.0 |
|||
KE SigmaE |
1.3 |
|||
KE C1 |
1.44 |
係数C1 |
||
KE C2 |
1.92 |
係数C1 |
||
KE Cmu |
0.09 |
係数Cmu |
||
KE Clip |
1.0e-6 |
|||
Viscosity Model |
K-Epsilon |
使用するモデル |
||
Heat Conductivity |
0.0257 |
W/m.K |
熱伝導度 |
|
Heat Capacity |
1.005e+3 |
J/kg.K |
比熱 |
|
Density |
1.166e+0 |
kg/m3 |
密度 |
メッシュ¶
メッシュについては、熱輸送なしのバックステップ流れと同様.
elmer シミュレーション設定¶
elmer シミュレーション設定ファイルを以下に示す.
!! ========================================================= !!
!! === steady state of back-step flow === !!
!! ========================================================= !!
include "./msh/model/mesh.names"
Header
CHECK KEYWORDS Warn
Mesh DB "." "msh/model"
Include Path ""
Results Directory "out/"
End
!! ------------------------------------------------- !!
!! --- [1] Simulation --- !!
!! ------------------------------------------------- !!
Simulation
Max Output Level = 3
Coordinate System = "Cartesian"
Coordinate Mapping(3) = 1 2 3
Simulation Type = "Steady State"
Steady State Max Iterations = 200
Post File = steady_ke.vtu
End
!! ------------------------------------------------- !!
!! --- [2] Solver & Equation --- !!
!! ------------------------------------------------- !!
Solver 1
Equation = k-epsilon
Procedure = "KESolver" "KESolver"
Stabilize = True
Linear System Solver = Direct
Linear System Direct Method = String "umfpack"
!! Linear System Iterative Method = BiCGStab
Linear System Max Iterations = 10000
Linear System Preconditioning = ILUT
Linear System Convergence Tolerance = 1.0e-5
Nonlinear System Max Iterations = 1
Nonlinear System Convergence Tolerance = 1.0e-5
Nonlinear System Relaxation Factor = 0.5
Nonlinear System Newton After Tolerance = 0.0
Nonlinear System Newton After Iterations = 10000
Steady State Convergence Tolerance = 1.0e-5
End
Solver 2
Equation = Navier-Stokes
Procedure = "FlowSolve" "FlowSolver"
Stabilize = True
Linear System Solver = Direct
Linear System Direct Method = String "umfpack"
!! Linear System Iterative Method = BiCGStab
Linear System Max Iterations = 10000
Linear System Convergence Tolerance = 1.0e-5
Linear System Preconditioning = ILUT
Nonlinear System Max Iterations = 1
Nonlinear System Convergence Tolerance = 1.0e-5
Nonlinear System Relaxation Factor = 0.5
Nonlinear System Newton After Tolerance = 0.0
Nonlinear System Newton After Iterations = 10000
Steady State Convergence Tolerance = 1.0e-5
End
Solver 3
Equation = "HeatEquations"
Procedure = "HeatSolve" "HeatSolver"
Variable = "Temperature"
Exec Solver = "Always"
Stabilize = True
Optimize Bandwidth = True
Linear System Solver = Iterative
Linear System Iterative Method = BiCGStab
Linear System Max Iterations = 500
Linear System Convergence Tolerance = 1.0e-8
Linear System Preconditioning = ILU0
Linear System Precondition Recompute = 1
Steady State Convergence Tolerance = 1.0e-5
Nonlinear System Convergence Tolerance = 1.0e-4
Nonlinear System Max Iterations = 1
Nonlinear System Newton After Iterations = 15
Nonlinear System Newton After Tolerance = 1.0e-4
Nonlinear System Relaxation Factor = 0.5
End
Equation 1
Name = "Fluid"
Active Solvers(3) = 2 1 3
Convection = Computed
End
!! ------------------------------------------------- !!
!! --- [3] body & materials --- !!
!! ------------------------------------------------- !!
Body 1
Name = "Fluid"
Target Bodies(1) = $ fluid
Equation = 1
Material = 1
Initial Condition = 1
End
Material 1
Name = "Air"
Viscosity = 1.0e-5 !! Pa.s
Density = 1.166e+0 !! kg/m3
KE SigmaK = 1.00
KE SigmaE = 1.30
KE C1 = 1.44
KE C2 = 1.92
KE Cmu = 0.09
KE Clip = Real 1.0e-6
Viscosity Model = K-Epsilon
!! Heat property !!
Heat Conductivity = 0.0257 !! W/m.K
Heat Capacity = 1.005e+3 !! J/kg.K
Reference Temperature = 293.15 !! K
End
!! ------------------------------------------------- !!
!! --- [4] initial boundary condition --- !!
!! ------------------------------------------------- !!
$ T_init = 293.15
$ T_wall = 393.15
Initial Condition 1
Velocity 1 = 0
Velocity 2 = 0
Temperature = $T_init
Kinetic Energy = 0.00457
Kinetic Dissipation = 1.0e-4
End
Boundary Condition 1
Name = "inlet"
Target Boundaries(1) = $ inlet
Velocity 1 = Variable Coordinate 2
Real MATC "6*(tx-1)*(2-tx)"
Velocity 2 = 0
Temperature = $T_init
Kinetic Energy = Real 0.00457
Kinetic Dissipation = Real 1.0e-4
End
Boundary Condition 2
Name = "outlet"
Target Boundaries(1) = $ outlet
Velocity 2 = 0.0
End
Boundary Condition 3
Name = "wall_x"
Target Boundaries(1) = $ wall_x
Temperature = $ T_wall
Noslip Wall BC = True
End
Boundary Condition 4
Name = "wall_y"
Target Boundaries(1) = $ wall_y
Temperature = $ T_wall
Noslip Wall BC = True
End