RANS ( Reynolds Averaged Navier-Stokes ) : k-εモデルについて¶
RANS ( Reynolds Averaged Navier-Stokes ) について¶
流体の基本方程式はNavier-Stokes方程式(NS方程式)である.
NS方程式は、対流項 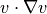 の影響で、短波長成分が生成される.例えば、ある空間的な流体波動、
の影響で、短波長成分が生成される.例えば、ある空間的な流体波動、 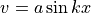 は、
は、
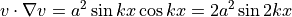
となるため、もとの2倍の波数の波が、対流項によるカップリングで生じてしまう.
これは、低波数モード(長波長)のエネルギーから、高波数(=短波長)のモードへとエネルギーカスケードすることを意味する.実際は、高波数モードでは、非線形的に粘性項による熱化が進むため、低波数→高波数→散逸、というエネルギーカスケードが生じる(プラズマでは逆のカスケードが生じうる!).数値シミュレーションとしては、適度な数値的拡散がないと、高波数モードが無限に生じてしまうため、乱流を含めたシミュレーションには、難しさがある.
この高波数構造(=渦)を、数値計算することを考える.近似度合いに応じて、いくつかの数値モデルがあり、以下に大別される.
DNS (直接数値計算:Direct Numerical Simulation)
LES (大局渦構造計算:Large Eddy Simulation)
RANS (レイノルズ平均ナビエ・ストークスモデル:Reynolds Averaged Navier-Stokes)
RANSは、時間・空間的に、渦と流れを分けて、別の輸送方程式として取り扱う.RANSの特徴は、
時間的に定常な解を解くのが得意
剥離などの時空間的にカップルした構造を計算するのが苦手
RANSのモデルに、
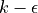 モデル
モデル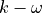 モデル
モデル
などがある.
k-εモデル¶
k-εモデルの特徴¶
k-εモデルは、通常のNS方程式に加えて、渦の運動エネルギー k、及び、渦のエネルギー散逸 ε も流れによって輸送するとみなして、流体と渦の時間的変化を解くモデルである.
k |
輸送される渦エネルギー(Kinetic Energy) |
ε |
輸送される渦の散逸度(Energy Dissipation) |
k-εモデルの特徴を以下にまとめる.
長所 |
簡便かつ安定に解くことができ、工学的応用が容易なモデル |
特別な追加パラメータ・近似等を用意しなくてよい |
|
短所 |
曲率を持った物体表面や、粘性低層のシミュレーションは近似である |
k, εの値はあくまでスケーリングから持ってきたアバウトな値であるため、精度を出しにくい |
基本方程式¶
k-εモデルのパラメータの決定¶
使用する k, εの境界条件や初期条件の値の決定は、以下の式を用いて行える[1-3].
渦強度 ( I )¶
![I = 0.16 Re_{[d_h]}^{-\dfrac{1}{8}}](../../../_images/math/4975c558d0ce4d09922545272aa94507f02881d3.png)
渦の特徴長さ ( l )¶
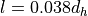
渦の運動エネルギー ( k )¶
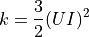
渦のエネルギー散逸 ( ε )¶
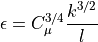
シミュレーションへの入力パラメータ計算¶
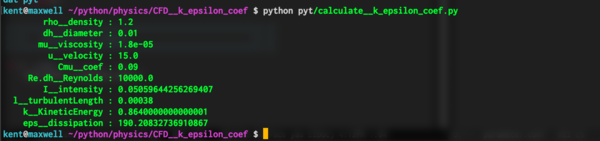
例えば、以下プログラムを用いて、計算し、k、εの初期値、境界値を固定値で指定する.(固定値(決め打ち)で良いのかはしらない.)
import os, sys, json
import numpy as np
# ========================================================= #
# === calculate__k_epsilon_coef.py === #
# ========================================================= #
def calculate__k_epsilon_coef( inpFile=None, outFile=None ):
# ------------------------------------------------- #
# --- [1] arguments --- #
# ------------------------------------------------- #
if ( inpFile is None ): inpFile = "dat/parameter.conf"
import nkUtilities.load__constants as lcn
inpFile = "dat/parameter.conf"
const = lcn.load__constants( inpFile=inpFile )
# ------------------------------------------------- #
# --- [2] const check --- #
# ------------------------------------------------- #
checkkeys = [ "rho__density", "dh__diameter", "mu__viscosity", "u__velocity" ]
for key in checkkeys:
if ( not( key in const ) ): sys.exit( " ERROR!!! cannot find {}.".format( key ) )
if ( not( "Cmu__coef" in const ) ):
print( "[calculate__k_epsilon_coef.py] default Cmu == 0.09 will be used. [CAUTION] " )
const["Cmu__coef"] = 0.09
# ------------------------------------------------- #
# --- [2] calculation --- #
# ------------------------------------------------- #
const["Re.dh__Reynolds"] = const["rho__density"] * const["u__velocity"] \
* const["dh__diameter"] / const["mu__viscosity"]
const["I__intensity"] = 0.16 * const["Re.dh__Reynolds"]**(-0.125)
const["l__turbulentLength"] = 0.038 * const["dh__diameter"]
const["k__KineticEnergy"] = 1.5 * ( const["u__velocity"] * const["I__intensity"] )**2
const["eps__dissipation"] = const["Cmu__coef"]**(0.75) * const["k__KineticEnergy"]**(1.5) \
/ const["l__turbulentLength"]
# ------------------------------------------------- #
# --- [3] output --- #
# ------------------------------------------------- #
if ( outFile is None ):
for key,item in const.items():
print( "{0:>20} : {1:<}".format( key, item ) )
else:
json.dump( const, outFile )
return()
# ========================================================= #
# === Execution of Pragram === #
# ========================================================= #
if ( __name__=="__main__" ):
calculate__k_epsilon_coef()
rho__density float 1.2e0
dh__diameter float 10e-3
mu__viscosity float 1.8e-5
u__velocity float 15.0
Cmu__coef float 0.09
Reference¶
[1] CFD online k epsilon model ( https://www.cfd-online.com/Wiki/Turbulence_free-stream_boundary_conditions )
[2] CFD online turbulence intensity ( https://www.cfd-online.com/Wiki/Turbulence_intensity )
[3] CFD online turbulence length scale ( https://www.cfd-online.com/Wiki/Turbulent_length_scale )
![Re_{[d_h]}](../../../_images/math/8ce8105a0c997851cd158d9d009bc6b1abe03e0b.png) )
)![Re_{[d_h]} = \dfrac{ \rho U d_h }{ \mu } = \dfrac{ U d_h }{ \nu }](../../../_images/math/16a63a27039fc647c70766a5337b7aac44754128.png)
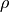 は質量密度 [kg/m3]、
は質量密度 [kg/m3]、 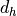 は水力直径 [m]、
は水力直径 [m]、 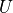 は平均流速 [m/s]、
は平均流速 [m/s]、 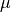 は粘度 [Pa s]、
は粘度 [Pa s]、 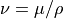 は動粘度 [m2/s] である.
は動粘度 [m2/s] である.