2次元円柱周り流れのシミュレーション (Navier-Stokes Eq.)¶
条件¶
2次元
解くべき方程式はNavier-Stokes方程式
領域は 縦 0.050 (m) 横 0.2 (m) の2次元矩形領域 ( (-0.1,-0.025)-(+0.1,+0.025) の領域 )
(x,y)=(-0.4, 0.0)に直径 0.010 (m) の円柱が存在する.
メッシュ¶
メッシュ生成コードは以下.
2次元円柱周り流れのメッシュ生成コード¶import numpy as np import os, sys import gmsh # ========================================================= # # === make__geometry === # # ========================================================= # def make__geometry( dimtags={} ): Lx,Ly = 0.2, 0.05 x0,y0,z0 = -0.5*Lx, -0.5*Ly, 0.0 xC,yC,zC = -0.2*Lx, 0.0, 0.0 rc = 0.10*min( Lx, Ly ) rect = gmsh.model.occ.addRectangle( x0, y0, z0, Lx, Ly ) circ = gmsh.model.occ.addDisk ( xC, yC, zC, rc, rc ) rect = [(2,rect)] circ = [(2,circ)] ret, fmap = gmsh.model.occ.cut( rect, circ, \ removeObject=True, removeTool=True ) dimtags["fluid"] = ret dimtags["circle"] = [(1,5)] dimtags["bottom"] = [(1,6)] dimtags["left"] = [(1,7)] dimtags["right"] = [(1,8)] dimtags["top"] = [(1,9)] return( dimtags ) # ========================================================= # # === 実行部 === # # ========================================================= # if ( __name__=="__main__" ): # ------------------------------------------------- # # --- [1] initialization of the gmsh --- # # ------------------------------------------------- # gmsh.initialize() gmsh.option.setNumber( "General.Terminal", 1 ) gmsh.option.setNumber( "Mesh.Algorithm" , 5 ) gmsh.option.setNumber( "Mesh.Algorithm3D", 4 ) gmsh.option.setNumber( "Mesh.SubdivisionAlgorithm", 0 ) gmsh.model.add( "model" ) # ------------------------------------------------- # # --- [2] Modeling --- # # ------------------------------------------------- # dimtags = {} dimtags = make__geometry( dimtags=dimtags ) gmsh.model.occ.removeAllDuplicates() gmsh.model.occ.synchronize() # ------------------------------------------------- # # --- [3] Mesh settings --- # # ------------------------------------------------- # mesh_from_config = True # from nkGMshRoutines/test/mesh.conf, phys.conf uniform_size = 0.05 if ( mesh_from_config ): meshFile = "dat/mesh.conf" physFile = "dat/phys.conf" import nkGmshRoutines.assign__meshsize as ams print( dimtags ) meshes = ams.assign__meshsize( meshFile=meshFile, physFile=physFile, \ dimtags=dimtags, target="surf" ) else: import nkGmshRoutines.assign__meshsize as ams meshes = ams.assign__meshsize( uniform=uniform_size, dimtags=dimtags ) # ------------------------------------------------- # # --- [4] post process --- # # ------------------------------------------------- # gmsh.model.occ.synchronize() gmsh.model.mesh.generate(2) gmsh.write( "msh/model.msh" ) gmsh.finalize()
mesh.conf¶# <names> key physNum meshType resolution1 resolution2 evaluation fluid 201 constant 3e-3 - - circle 105 constant 0.0 - - bottom 101 constant 0.0 - - left 102 constant 0.0 - - right 103 constant 0.0 - - top 104 constant 0.0 - -
phys.conf¶# <names> key type dimtags_keys physNum fluid surf [fluid] 201 circle line [circle] 105 bottom line [bottom] 101 left line [left] 102 right line [right] 103 top line [top] 104
メッシュの様子は以下.

シミュレーション .sif ファイル¶
elmer シミュレーションコードは以下.
2次元円柱周り流れのシミュレーションコード¶include "./msh/model/mesh.names" Header CHECK KEYWORDS Warn Mesh DB "." "msh/model" Include Path "" Results Directory "out/" End Simulation Max Output Level = 3 Coordinate System = string "Cartesian" Coordinate Mapping(3) = 1 2 3 Simulation Type = "Transient" TimeStepping Method = BDF BDF Order = 2 Timestep sizes(1) = 50e-3 Timestep Intervals(1) = 200 Steady State Max Iterations = 30 Post File = output.vtu End Constants Gravity(4) = 0 0 -1 9.82 !! m/s^2 End Solver 1 Equation = Navier-Stokes Linear System Solver = Iterative Linear System Scaling = Logical False Linear System Direct Method = UMFPACK Linear System Iterative Method = BiCGStab Linear System Convergence Tolerance = 1.0e-6 Linear System Max Iterations = 3000 Linear System Preconditioning = ILUT Nonlinear System Convergence Tolerance = Real 1.0e-7 Nonlinear System Max Iterations = Integer 500 Nonlinear System Relaxation Factor = Real 0.8 Nonlinear System Newton After Iterations = 15 Nonlinear System Newton After Tolerance = 1.0e-3 Steady State Convergence Tolerance = 1.0e-6 stabilize = True Div Discretization = True End Body 1 Name = "Fluid" Target Bodies(1) = $fluid Equation = 1 Material = 1 End Equation 1 Name = "Fluid" Active Solvers(1) = 1 Navier-Stokes = True End Material 1 Name = "Air" Density = 1.2e0 !! kg/m3 Viscosity = 1.0e-5 End Boundary Condition 1 Name = "left" Target Boundaries(1) = $left Velocity 1 = 0.05 Velocity 2 = 0 Velocity 3 = 0 End Boundary Condition 2 Name = "right" Target Boundaries(1) = $right Pressure = 0.0 End Boundary Condition 3 Name = "top" Target Boundaries(1) = $top Velocity 1 = 0 Velocity 2 = 0 Velocity 3 = 0 End Boundary Condition 4 Name = "bottom" Target Boundaries(1) = $bottom Velocity 1 = 0 Velocity 2 = 0 Velocity 3 = 0 End
境界条件は、
左側=上流面
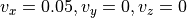
右側=下流面:圧力ゼロ (
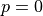 )
)側面-固定癖:流速ゼロ (
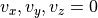 )
)
シミュレーション結果¶
シミュレーション結果の例.
webサイトではカルマン渦ができているが、自分の環境ではカルマン渦ができていない.
おそらくレイノルズ数の関係.レイノルズ数が低くて(粘性を下げてもカルマン渦ができないことから数値粘性ではないかと思われる)
メッシュを細かくきる必要があるかも.
