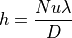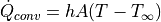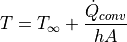円筒物体周りの流れによる強制空冷について ( その１ )¶

図のような体系を考える．

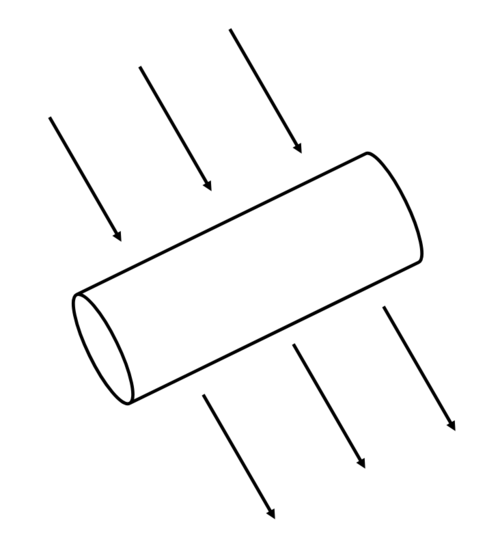
../../_images/schematic__forcedCollingAroundCylinder.png

円筒形状の物体（冷却対象）に直行して流体（水、空気、etc.）が流れて強制対流によって冷却される．この場合の熱伝達率、及び、冷却対象の定常状態の温度を考える．内容については文献[1]を参考にしている．

基本式¶

以下に計算に用いる基本式を示す．

Reynolds数の計算¶

直径Dの円筒まわりの流れに対するReynold数を計算する．

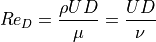
$Re_D = \dfrac{ \rho U D }{ \mu } = \dfrac{ UD }{ \nu }$

ここで、もちろん、Uは流速 [m/s], Dは円筒の直径 [m]、 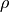$\rho$ は流体の密度 [kg/m3]、 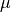$\mu$ は粘性率 [Pa s] であり、 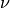$\nu$ は動粘度 [m2/s] である．

Nusselt数の計算¶

Nusselt数 Nu は、Hilpert-Kundsen-Katzの式より、

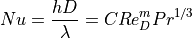
$Nu = \dfrac{ h D }{ \lambda } = C Re_D^m Pr^{1/3}$

ここで、熱伝達率 h [W/m2K], 熱伝導度 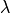$\lambda$ 、プラントル数 Pr を用いている．また、使用している係数 C, m は参考文献[1][2][3] より見つけることができる．

たとえば、以下である．

**Coefficients of Hilpert-Kundsen-Katz formula**¶
Re	C	m
0.4-4	0.989	0.330
4-40	0.911	0.385
40-4000	683	466
4000-40000	0.193	0.618
40000-400000	0.027	0.805

熱伝達率の計算¶

熱伝達率は、Nusselt数より求めることができる．

$h = \dfrac{ Nu \lambda }{ D }$

温度の計算¶

Newtonの冷却法則より、求めることができる．

$\dot{ Q }_{conv} = hA ( T - T_{\infty} )$

変形すれば、陽に、冷却対象の温度として、次が導ける．

$T = T_{\infty} + \dfrac{ \dot{ Q }_{conv} }{ hA }$

計算例（シンプル）¶

物性値は温度依存性をもつ．そのため、一度の冷却対象の温度の算出で、系の定常状態は決定されない．一方、initial guess として、また、計算手法を記す目的で、反復をしない計算例を以下に挙げる．例えば、流速 U=10 m/s, 円筒の直径 D=15 mm、を空気で冷やすことを考えれば、Reynolds数は

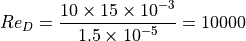
$Re_D = \dfrac{ 10 \times 15 \times 10^{-3} }{ 1.5 \times 10^{-5} } = 10000$

Nusselt数は、空気のPrandtl数 0.7 、及び、係数 C=0.193, m=0.618 を用いて、

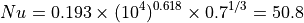
$Nu = 0.193 \times ( 10^4 )^{0.618} \times 0.7^{1/3} = 50.8$

これより、熱伝達率は、

$h = \dfrac{ 50.8 \times 0.025 }{ 15 \times 10^{-3} } = 84.6 \mathrm{[W/m^2K]}$

無限遠での空気の温度を 25 ℃として、発熱量を 100 W, 円筒長さが 100 mmとすれば、表面積Aはおよそ A=0.005 であるので、

$T = 25 + \dfrac{ 100 }{ 84.6 \times 0.005 } = 25 + 236.4 = 261.4 [C]$

シンプル計算用のスクリプト¶

スクリプト¶

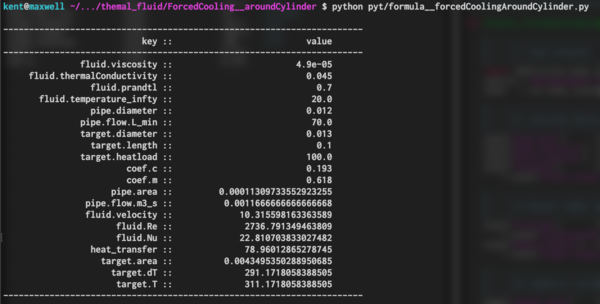
上記計算を実行するスクリプトは以下である．

formula__forcedCoolingAroundCylinder.py¶

import numpy as np

# ========================================================= #
# ===  formula__forcedCoolingAroundCylinder.py          === #
# ========================================================= #

def formula__forcedCoolingAroundCylinder():

    # ------------------------------------------------- #
    # --- [1] load constants                        --- #
    # ------------------------------------------------- #
    import nkUtilities.load__constants as lcn
    cnsFile = "dat/parameter.conf"
    const   = lcn.load__constants( inpFile=cnsFile )
    
    # ------------------------------------------------- #
    # --- [2] calculate Reynolds Number             --- #
    # ------------------------------------------------- #
    const["pipe.area"]       = const["pipe.diameter"]**2 * np.pi / 4
    const["pipe.flow.m3_s"]  = const["pipe.flow.L_min"] * 1e-3 / 60.0
    const["fluid.velocity"]  = const["pipe.flow.m3_s"] / const["pipe.area"]
    const["fluid.Re"]        = const["fluid.velocity"] * const["target.diameter"] \
        / const["fluid.viscosity"]

    # ------------------------------------------------- #
    # --- [3] Nusselt Number & heat transfer        --- #
    # ------------------------------------------------- #
    const["fluid.Nu"]        = const["coeff.c"] * const["fluid.Re"]**const["coeff.m"] \
        * const["fluid.prandtl"] ** ( 1./3. )
    const["heat_transfer"]   = const["fluid.Nu"] * const["fluid.thermalConductivity"] \
        / const["target.diameter"]

    # ------------------------------------------------- #
    # --- [4] tempature estimation                  --- #
    # ------------------------------------------------- #
    const["target.area"]     = 2.0*( np.pi / 4 * const["target.diameter"]**2 ) \
        + np.pi * const["target.diameter"] * const["target.length"]
    const["target.dT"]       = const["target.heatload"] \
        / ( const["heat_transfer"] * const["target.area"] )
    const["target.T"]        = const["fluid.temperature_infty"] + const["target.dT"]

    # ------------------------------------------------- #
    # --- [5] display results                       --- #
    # ------------------------------------------------- #
    print( "\n" + "-" * 70 )
    print( "{0:>30} :: {1:>30}".format( "key", "value" ) )
    print( "-" * 70 )
    for key,value in const.items():
        print( "{0:>30} :: {1:>30}".format( key, value ) )
    print( "-" * 70 + "\n" )
        
    return()


# ========================================================= #
# ===   Execution of Pragram                            === #
# ========================================================= #

if ( __name__=="__main__" ):
    formula__forcedCoolingAroundCylinder()

parameter.confで計算条件を与える．

実行結果¶

実行結果は例えば、以下．

../../_images/script_result__forcedCollingAroundCylinder.png

Reference¶

[1] 小山敏行, 例題で学ぶ伝熱工学, 森北出版, 2012 [2] R.Helpert Warmeabgabe von geheizen Drahten und Rohren, Forsch. Geb Ingenieurwes vol.4, 1933 [3] J.D. Kundsen, D.L.Katz Fluid Dynamics and Heat Transfer, McGraw-Hill, 1958