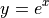Runge-Kutta 法¶
Runge-Kutta 法 ( Runge-Kutta Method ) は代表的な常微分方程式の数値解法である. 予測子・修正子法 ( predictor-Corrector Method )を用いて,高精度かつロバストに数値積分可能である. Runge-Kutta 法には,段数,精度,係数を任意に設定することができるため,一般に呼ばれる場合,大体4次精度の古典的手法を指すことが多い.
数値解法¶
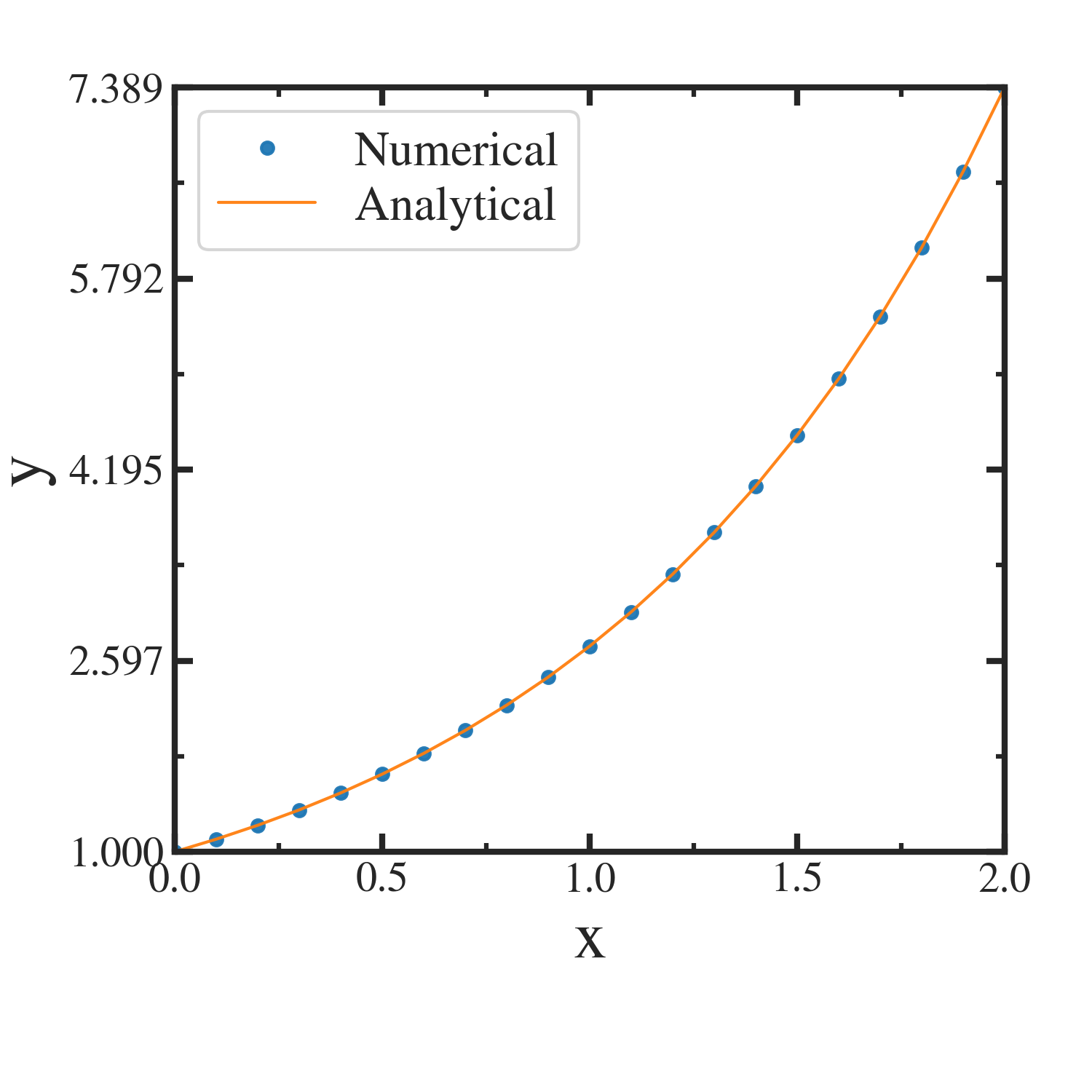
次の常微分方程式を解くことを考える.
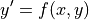
初期値を 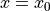 において
において 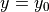 とする.微小区間
とする.微小区間 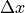 によって離散化すれば,常微分方程式の数値積分解を次の式から得ることができる ( 4th-order Runge-Kutta Method ).
によって離散化すれば,常微分方程式の数値積分解を次の式から得ることができる ( 4th-order Runge-Kutta Method ).
![x_{n+1} &= x_{n} + \Delta x \\
y_{n+1} &= y_{n} + \dfrac{\Delta x}{6} [ k_1 + 2k_2 + 2k_3 + k_4 ]](../../_images/math/52d82439b5a245136e48bbe43b093000f7e04f9a.png)
ここで,係数 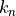 は以下の式から得る.
は以下の式から得る.
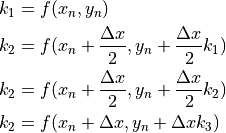
実装¶
Fortran90で実装した.
前提として,微分方程式の被数値積分対象である右辺 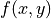 は解析的に得られるとする.
ここで,
は解析的に得られるとする.
ここで, 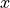 の離散化の間隔は任意としている.大した計算負荷ではないが,
の離散化の間隔は任意としている.大した計算負荷ではないが, 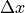 の計算は等間隔であれば主 Runge-Kutta ループ外部へ出すことができる.
の計算は等間隔であれば主 Runge-Kutta ループ外部へ出すことができる.
まず,メインルーチンを示す.ここでは,x, yを離散化,初期化して,初期値 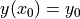 を代入する. Runge-Kutta ソルバーを呼び出し,数値積分した後,画面及びファイルへ出力する.
を代入する. Runge-Kutta ソルバーを呼び出し,数値積分した後,画面及びファイルへ出力する.
program main
use RKGMethodMod, only : RungeKutta4th
implicit none
integer , parameter :: cLen = 300
integer , parameter :: nData = 21
double precision, parameter :: xMin = 0.d0
double precision, parameter :: xMax = 2.d0
integer :: i
double precision :: xn(nData), yn(nData)
character(cLen) :: datFile='dat/out.dat'
! ------------------------------------------------------ !
! --- [1] preparation :: initial settings --- !
! ------------------------------------------------------ !
do i=1, nData
xn(i) = ( xMax - xMin ) / dble( nData-1 ) * dble(i-1) + xMin
yn(i) = 0.d0
enddo
yn(1) = 1.d0
! ------------------------------------------------------ !
! --- [2] Runge Kutta ( 4th-order ) --- !
! ------------------------------------------------------ !
call RungeKutta4th( xn, yn, nData )
! ------------------------------------------------------ !
! --- [3] output results --- !
! ------------------------------------------------------ !
do i=1, nData
write(6,*) i, xn(i), yn(i)
enddo
open( 50, file=trim(datFile), status='replace', form='formatted' )
do i=1, nData
write(50,*) i, xn(i), yn(i)
enddo
close(50)
return
end program main
次に, Runge-Kutta ソルバーのモジュールを示す.
区間 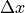 における
における 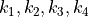 を求め,
を求め,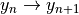 の数値積分を反復するルーチンと,右辺を計算する関数がある.
の数値積分を反復するルーチンと,右辺を計算する関数がある.
module RKGMethodMod
contains
! ====================================================== !
! === Runge-Kutta ( 4th-order ) === !
! ====================================================== !
subroutine RungeKutta4th( xn, yn, nData )
implicit none
integer , intent(in) :: nData
double precision, intent(inout) :: xn(nData), yn(nData)
integer :: i
double precision :: k1, k2, k3, k4, dx, hdx
double precision, parameter :: onesixth = 1.d0 / 6.d0
do i=1, nData-1
dx = xn(i+1) - xn(i)
hdx = 0.5d0*dx
k1 = rhs( xn(i) , yn(i) )
k2 = rhs( xn(i)+hdx, yn(i)+hdx*k1 )
k3 = rhs( xn(i)+hdx, yn(i)+hdx*k2 )
k4 = rhs( xn(i)+ dx, yn(i)+ dx*k3 )
yn(i+1) = yn(i) + onesixth*dx*( k1 + 2.d0*k2 + 2.d0*k3 + k4 )
enddo
return
end subroutine RungeKutta4th
! ====================================================== !
! === evaluate R.H.S. === !
! ====================================================== !
function rhs( x, y )
implicit none
double precision, intent(in) :: x, y
double precision :: rhs
rhs = y
return
end function rhs
end module RKGMethodMod
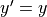 の微分方程式を初期値
の微分方程式を初期値 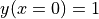 のもとで解くことを考える.
解析的には,
のもとで解くことを考える.
解析的には,