熱伝導方程式における有限要素法解析のいろいろ

熱伝導方程式 ( Heat Transfer Equation )

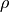前項では，もっとも簡単な例として，熱拡散方程式の定常解を取り扱った． ここでは，より一般的な熱解析へ有限要素法を適用することを考え，熱伝導方程式における定式化を考える． 等方的な熱伝導度 \kappa , 比熱 c ，質量密度 \rho を有する物質における温度 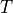T の変化を示す熱伝導方程式は，

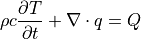
\rho c \dfrac{ \partial T }{ \partial t } + \nabla \cdot q = Q

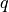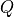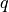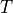と記述される．ここで， q ， Q はそれぞれ熱流束，体積内で生成される熱を示している．ここで，熱流朿 q 及び温度 T には Hook の法則，

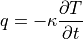
q = - \kappa \dfrac{ \partial T }{ \partial t }

が成り立ち，

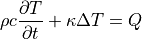
\rho c \dfrac{ \partial T }{ \partial t } + \kappa \Delta T = Q

が，一般的な熱伝導方程式となる．

有限要素法における各項の記述

各要素において，形状関数を用いた有限要素法による表記を導入する．

T &= \sum_k N_k T_k = [N] \{ T \} \\ [N] &= [ N_1 \ N_2 \ \cdots ] \\ \{ T \} &= \{ T_1 \ T_2 \ \cdots \}

温度勾配を計算しておくと，

\nabla T = \begin{bmatrix} \partial T / \partial x \\ \partial T / \partial y \\ \partial T / \partial z \\ \end{bmatrix} = \begin{bmatrix} \partial N_1 / \partial x & \partial N_2 / \partial x & \cdots \\ \partial N_1 / \partial y & \partial N_2 / \partial y & \cdots \\ \partial N_1 / \partial z & \partial N_2 / \partial y & \cdots \\ \end{bmatrix} \{ T \} = [B] \{ T \}

と， [B] を用いて書くことができる．これを用いれば Hook の法則は

\{ q \} = - \kappa [B] \{ T \}

とかける．

次に，上述の熱伝導方程式に， Galerkin 法による重み付き残差法 (WRM) を導入し，有限要素法における熱伝導方程式の表式を導く．

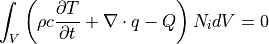
\int_V \left( \rho c \dfrac{ \partial T }{ \partial t } + \nabla \cdot q - Q \right) N_i dV = 0

から， Green の定理より，

\int_V \rho c \dfrac{ \partial T }{ \partial t } N_i dV - \int_V [ \dfrac{\partial N_i}{\partial x} \ \dfrac{\partial N_i}{\partial y} \ \dfrac{\partial N_i}{\partial z} ] \{ q \} dV = \int_V Q N_i dV - \int_S \{ q \}^T \{ n \} N_i dS

各面での境界条件を導入すれば，

\int_V \rho c \dfrac{ \partial T }{ \partial t } N_i dV - \int_V [ \dfrac{\partial N_i}{\partial x} \ \dfrac{\partial N_i}{\partial y} \ \dfrac{\partial N_i}{\partial z} ] \{ q \} dV &= \int_V Q N_i dV \\ &- \int_{S_1} \{ q \}^T \{ n \} N_i dS + \int_{S_2} \{ q_s \} N_i dS \\ &- \int_{S_3} h( T-T_e ) N_i dS - \int_{S_4} ( \sigma \epsilon T^4 - \alpha q_r ) N_i dS

である．各要素におけるN本の式(i=1,2,...,N)をまとめると，

\int_V \rho c [N]^T [N] \dfrac{ \partial [T] }{ \partial t } dV + \int_V k [B]^T [B] [T] dV &= \int_V Q [N]^T dV \\ &- \int_{S_1} \{ q \}^T \{ n \} [N] dS + \int_{S_2} \{ q_s \} [N] dS \\ &- \int_{S_3} h [N]^T [N] \{ T \} dS + \int_{S_3} h T_e [N]^T dS \\ &- \int_{S_4} \sigma \epsilon T^4 [N]^T dS + \int_{S_4} \alpha q_r [N]^T dS

これを各項毎に整理すると，以下のようになる．

[C] \{ \dot{T} \} + ( [K_c] + [K_h] + [K_r] )\{ T \} = \{R_T\} + \{R_Q\} + \{R_q\} + \{R_h\} + \{R_r\}

ここで，

[C] &= \int_V \rho c [N]^T [N] dV \\ [K_c] &= \int_V k [B]^T [B] dV \\ \{ R_Q \} &= \int_V Q [N]^T dV \\ \{ R_T \} &= \int_{S_1} \{ q \}^T \{ n \} [N] dS \\ \{ R_q \} &= \int_{S_2} \{ q_s \} [N] dS \\ [K_h] &= \int_{S_3} h [N]^T [N] dS \\ \{ R_h \} &= \int_{S_3} h T_e [N]^T dS \\ [K_r]\{ T \} &= \int_{S_4} \sigma \epsilon T^4 [N]^T dS \\ \{ R_r \} &= \int_{S_4} \alpha q_r [N]^T dS

とおいている．

一般化された方程式系から解析モデルに合わせて必要な項のみ含めば，所望の有限要素解析を行うことができる． 例えば，以下のようなものである．

定常線形モデル

( [K_c] + [K_h] )\{T\} = \{R_Q\} + \{R_q\} + \{R_h\}

時間変化無し，かつ，線形の問題（解くべき方程式が温度の1次(=定数倍)の項しかもたない）の場合，上記5項以下の方程式で記述できる． ちなみに，前項で解いた定常熱拡散方程式は，上記の定常線形モデルのうち，対流境界条件を持たない場合( [K_h]=0, 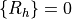\{R_h\}=0 )である．

定常線形モデルの場合，方程式系の係数が温度Tによって変化することがなく，また時間変化を解く必要もないため，上記 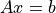Ax=b として表記された線形連立方程式を一度だけ行列反転すれば求解できる．

定常非線形モデル

( [K_c] + [K_h] + [K_r] )\{T\} = \{R_Q(T)\} + \{R_q(T)\} + \{R_h(T)\} + \{R_r(T)\}

問題が求めたい物理量によって，各項が変化する(1次以上の効果)項が入っている定常問題が定常非線形モデルに相当する．熱伝導方程式の具体例としては，溶鉱炉内の溶けた鉄等， 放射項 ( Stefan-Boltzmann 則によって温度の４乗に比例する )が無視できない場合がある．このように，支配方程式内の他の項が求めたい物理量の関数になっている場合，定常線形モデルと同様にして解くことはできない．しかし，例えば，非線形項が含む温度Tを定数と捉えて，K-行列及び右辺ベクトルを計算すれば，

[K](T=T^{n}) \{ T^{n+1} \} = \{ R \}(T=T^{n})

定常線形モデルとして解くことができる．これは，適当な温度 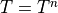T=T^n を仮定し，非線形項を定数として考えて（線形化して）求めた解ので，得られた解 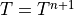T=T^{n+1} は真の解ではない．しかし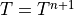， T=T^{n+1} が真の解により近いベターな解が得られたと仮定すれば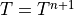， T=T^{n+1} から [K](T=T^{n+1}), \{R\}(T=T^{n+1}) を再度計算し，もう一度同様な方程式，

[K](T=T^{n+1}) \{ T^{n+2} \} = \{ R \}(T=T^{n+1})

を解けば，「より真の解に近いベターな解」から出発した「もうちょっと真の解に近いよりベターな解」を得ることができるかもしれない．結局はこれを十分大きな回数繰り返し，許容誤差

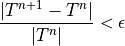
\dfrac{ | T^{n+1} - T^{n} | }{ | T^{n} | } < \epsilon

となるような解に収束すれば，真の非線形解に十分な近い数値解を得ることができる． このように，非線形問題であっても，線形化して十分な回数反復することで有限要素解析できる．

非定常線形モデル

[C]\{\dot{T}(t)\} + ( [K_c] + [K_h](t) )\{T(t)\} = \{R_Q(t)\} + \{R_q(t)\} + \{R_h(t)\}

熱平衡状態へ遷移するまでの過渡的な解析を行いたい場合，時間微分項を含んだ熱伝導方程式を解く必要がある． 線形項のみを含んでいる場合についてまず考える． 時間変化項を，単純な1次精度後退差分式によって置き換えると，

[ \dot{T} ](t) \sim \dfrac{ [T](t) - [T](t-\Delta t) }{ \Delta t }

であるから，

[T](t) = [T](t-\Delta t) + [\dot{T}](t) \Delta t

として，時間ステップを進める．つまり，線形定常モデルとして解析した解を用いて時間積分を順次行なっていくことになる．

非定常非線形モデル

[C]\{\dot{T}(t)\} + ( [K_c](T) + [K_h](T,t) + [K_r](T) )\{T(t)\} = \{R_Q(T,t)\} + \{R_q(T,t)\} + \{R_h(T,t)\} + \{R_r(T,t)\}

これは，非線形モデルと非定常モデルの合わせ技であるから，この二つを独立に反復すれば良い．つまり，非線形モデルを線形化・反復することによって求解し，そこで得た非線形解を用いて時間ステップすれば良い．つまり，非線形解を解くのにループが一つ，それを微小時間ステップ毎に何度も繰り返し，所望の時間経過まで過渡問題を解析する．

参考文献