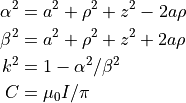環状電流がつくる磁場

環状電流がつくる磁場は楕円積分を用いて計算することができる． Classical Electromagnetism, J.D.Jackson (1962) に極座標系における計算が記述されており， Simple Analytic Expressions for the Magnetic Field of a Circular Current Loop, J.Simpson et.al.,(2001) に Cartesian 及び 円筒座標系における表式が記載されている．

以下に，環状電流がつくる磁場についてまとめる．

極座標系におけるベクトルポテンシャルの表式

まず， J.D.Jackson pp.181--183 に記述されている環状電流がつくるベクトルポテンシャルは以下のように表される．

A_{\psi} ( r, \theta ) &= \dfrac{ \mu_0 I a }{ 4 \pi } \int^{ 2 \pi }_{0} \dfrac{ cos \psi ^{\prime} d \psi ^{\prime} }{ \sqrt{ a^2 + r^2 - 2 a r \sin \theta \cos \psi ^{\prime} } } \\ &= \dfrac{ \mu_0 }{ 4 \pi } \dfrac{ 4 I a }{ \sqrt{ a^2 + r^2 + 2 a r \sin \theta } } \left[ \dfrac{ (2-k^2) K(k^2) - 2 E(k^2) }{ k^2 } \right]

ここで，第1種 / 第2種 完全楕円積分 ( 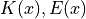K(x), E(x) ) の引数部分である 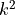k^2 は，

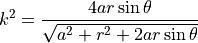
k^2 = \dfrac{ 4 a r \sin \theta }{ \sqrt{ a^2 + r^2 + 2 a r \sin \theta } }

である．

極座標系における環状電流がつくる磁場

磁場はベクトルポテンシャルの回転より求めることができ，極座標系では以下のように表される．

B_r &= \dfrac{ 1 }{ r \sin \theta } \dfrac{ \partial }{ \partial \theta } ( \sin \theta A_{\psi} ) \\ &= \dfrac{ C a^2 \cos \theta }{ \alpha^2 \beta } E (k^2) \\ \\ B_\theta &= - \dfrac{1}{r} \dfrac{ \partial }{ \partial r } ( r A_{\psi} ) \\ &= \dfrac{ C }{ 2 \alpha^2 \beta \sin \theta } \left[ ( r^2 + a^2 \cos 2 \theta ) E (k^2) - \alpha^2 K(k^2) \right] \\ \\ B_\psi &= 0

ここで，

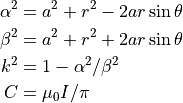
\alpha^2 &= a^2 + r^2 - 2 a r \sin \theta \\ \beta^2 &= a^2 + r^2 + 2 a r \sin \theta \\ k^2 &= 1 - \alpha^2 / \beta^2 \\ C &= \mu_0 I / \pi

としている．

Cartesian 座標系における環状電流がつくる磁場

B_x &= \dfrac{ C x y }{ 2 \alpha^2 \beta \rho^2 } \left[ ( a^2 + r^2 ) E(k^2) - \alpha^2 K(k^2) \right] \\ \\ B_y &= \dfrac{ C y z }{ 2 \alpha^2 \beta \rho^2 } \left[ ( a^2 + r^2 ) E(k^2) - \alpha^2 K(k^2) \right] \\ \\ B_z &= \dfrac{ C }{ 2 \alpha^2 \beta } \left[ ( a^2 - r^2 ) E(k^2) + \alpha^2 K(k^2) \right]

ここで，

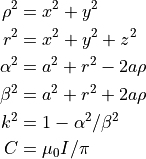
\rho^2 &= x^2 + y^2 \\ r^2 &= x^2 + y^2 + z^2 \\ \alpha^2 &= a^2 + r^2 - 2 a \rho \\ \beta^2 &= a^2 + r^2 + 2 a \rho \\ k^2 &= 1 - \alpha^2 / \beta^2 \\ C &= \mu_0 I / \pi

としている．

Cylindrical 座標系における環状電流がつくる磁場

B_\rho &= \dfrac{ C z }{ 2 \alpha^2 \beta \rho } \left[ ( a^2 + \rho^2 + z^2 ) E(k^2) - \alpha^2 K (k^2) \right] \\ \\ B_\theta &= 0 \\ \\ B_z &= \dfrac{ C }{ 2 \alpha^2 \beta } \left[ ( a^2 - \rho^2 - z^2 ) E(k^2) + \alpha^2 K (k^2) \right]

ここで，

\alpha^2 &= a^2 + \rho^2 + z^2 - 2 a \rho \\ \beta^2 &= a^2 + \rho^2 + z^2 + 2 a \rho \\ k^2 &= 1 - \alpha^2 / \beta^2 \\ C &= \mu_0 I / \pi

としている．