3次元磁力線追跡¶

流線追跡の定式化¶

まず，ベクトルが示す直線の方程式は一般に次式で表される．

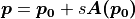
$\bm{p} = \bm{p_0} + s \bm{A(p_0)}$

ここで，任意の空間上の 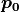$\bm{p_0}$ に存在するベクトル場を 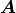$\bm{A}$ とし，直線は座標 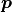$\bm{p}$ 上に描かれる．ここで， $s$ は媒介変数表示用のパラメータである．

ベクトル場が作る流線を描く( 追跡する ) ためには，流線を無限小長さの直線として取り扱えば良い．つまり，計算機上で数値的に流線を追跡するためには，上記直線の方程式を用いて 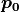$\bm{p_0}$ におけるベクトル場 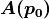$\bm{A(p_0)}$ から，ごく近傍の点 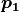$\bm{p_1}$ の座標位置を計算する．次は 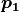$\bm{p_1}$ を出発点とし，同様にベクトル場 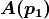$\bm{A(p_1)}$ から，ごく近傍の点 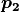$\bm{p_2}$ の座標位置をする．以下，これを繰り返せばあるベクトル場が作る流線を追跡することができる．

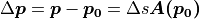
$\Delta \bm{p} = \bm{p} - \bm{p_0} = \Delta s \bm{A(p_0)}$

が解くべき方程式となる．上式より，任意の初期位置を通る流線は，Runge-Kutta法などを用いて数値積分することで，追跡することができる．

3次元磁力線追跡の例¶

電磁気学における静磁場は，各空間における磁場ベクトル分布が既知であれば，磁力線を可視化することができる．

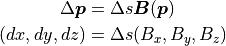
$\Delta \bm{p} &= \Delta s \bm{B}(\bm{p}) \\ ( dx, dy, dz ) &= \Delta s ( B_x, B_y, B_z )$

を数値的に解けば良い．例題として，次のベクトル場を考える．

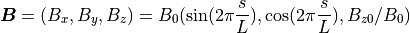
$\bm{B} = ( B_x, B_y, B_z ) = B_0 ( \sin ( 2 \pi \dfrac{s}{L}), \cos ( 2 \pi \dfrac{s}{L}), B_{z0} / B_0 )$

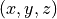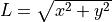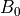但し，位置 $(x,y,z)$ における， $L=\sqrt{x^2 + y^2}$ とし， $B_0$ は磁場強度パラメータ， $s$ は弧長である．

ここで用いた磁場分布は， ( B_x, B_y ) が媒介変数表示の円の方程式であることから，z方向に移動する螺旋を描くはずである．

3次元磁力線追跡の数値計算¶

以下に3次元磁力線追跡コードを掲載する．

3次元磁力線追跡結果¶

上記例題の3次元追跡結果を以下に示す．