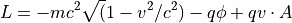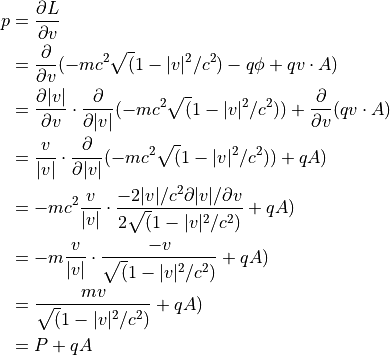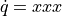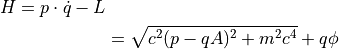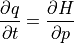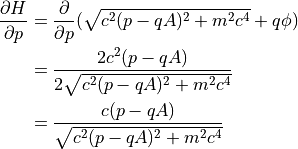Single Particle Dynamics ( 単粒子力学 ) について

Newton-Lorentz Eqs. の一般化

電磁ポテンシャル 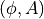(\phi,A) 中の荷電粒子の挙動は Newton-Lorentz 方程式系で表すことができる．

\dfrac{ dP }{ dt } = q [ E + v \times B ]

ここで，電磁ポテンシャル 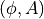(\phi,A) はMaxwell Eq.によって規定されている．

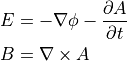
E &= - \nabla \phi - \dfrac{ \partial A }{ \partial t } \\ B &= \nabla \times A

ここで， Cartesian 座標系等の特定の座標系ではなく，座標系によらない取り扱いをするために， Hamilton 方程式による記述を考える．

Lagrangean の導出

Lagrangean L(q,\dot{q},t) は以下で与えられる．

L = - mc^2 \sqrt( 1 - v^2 / c^2 ) - q \phi + q v \cdot A

Hamiltonian による単粒子力学の定式化

ここでは， Lagrangean からの Hamiltonian の導出を考える．まず，

p &= \dfrac{\partial L}{ \partial v } \\ &= \dfrac{\partial }{ \partial v } ( - mc^2 \sqrt( 1 - |v|^2 / c^2 ) - q \phi + q v \cdot A ) \\ &= \dfrac{\partial |v| }{ \partial v } \cdot \dfrac{\partial }{ \partial |v| } ( - mc^2 \sqrt( 1 - |v|^2 / c^2 ) ) + \dfrac{\partial }{ \partial v } ( q v \cdot A ) \\ &= \dfrac{ v }{ |v| } \cdot \dfrac{\partial }{ \partial |v| } ( - mc^2 \sqrt( 1 - |v|^2 / c^2 ) ) + qA ) \\ &= - mc^2 \dfrac{ v }{ |v| } \cdot \dfrac{ - 2|v|/c^2 \partial |v| / \partial v }{ 2 \sqrt( 1 - |v|^2 / c^2 ) } + qA ) \\ &= - m \dfrac{ v }{ |v| } \cdot \dfrac{ - v }{ \sqrt( 1 - |v|^2 / c^2 ) } + qA ) \\ &= \dfrac{ m v }{ \sqrt( 1 - |v|^2 / c^2 ) } + qA ) \\ &= P + qA

である．次に，

\dot{q} = xxx

これらより，

H = p \cdot \dot{q} - L \\ &= \sqrt{ c^2 ( p - qA )^2 + m^2 c^4 } + q \phi

となる．

Hamiltonian から Newton-Lorentz Eqs. への帰着

当然， Hamiltonian から Hamilton の正準方程式を計算すると， Newton-Lorentz Eqs. へ帰着するべきである．

\dfrac{ \partial q }{ \partial t } = \dfrac{ \partial H }{ \partial p }

を考えると， \gamma = \sqrt{ P^2 + m^2c^2 } / mc を用いて，

\dfrac{ \partial H }{ \partial p } &= \dfrac{ \partial }{ \partial p } ( \sqrt{ c^2 ( p - qA )^2 + m^2 c^4 } + q \phi ) \\ &= \dfrac{ 2 c^2 ( p - qA ) }{ 2 \sqrt{ c^2 ( p - qA )^2 + m^2 c^4 } } \\ &= \dfrac{ c ( p - qA ) }{ \sqrt{ c^2 ( p - qA )^2 + m^2 c^4 } }